656
Stephanie R. Land and Jerome H. Friedman
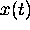. We propose a nonlinear regularized regression technique,
variable fusion. Variable fusion produces models of a simple
parsimonious form, readily explained to the non-statistician and
possibly affording savings in data collection. In addition, variable
fusion models perform well in terms of prediction. In this paper we assume
that the quantity y is real and single-valued and the pattern 
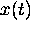is a ``signal'', i.e., the space of index values t is
one-dimensional, although we describe the generalization of the method
to a multidimensional index space. We use the patterns as the
predictors of y. The patterns generally originate as analog signals
and are measured at a large set of discrete index values, giving rise
to a correspondingly large set of predictor variables. The problem is
therefore ill-posed and requires regularization. Variable fusion
regularizes by exploiting the spatial nature of the predictor variable
index through powerful variable bandwidth nonlinear smoothing analogs
based on adaptive splines. We compare this method with partial
least squares, ridge regression and cubic spline smoothing. The first
two of these methods apply regularization that is equivariant to the
labeling of the predictors. They therefore ignore the spatial nature
of the predictor index. The latter method, cubic spline smoothing, is
linear and cannot as readily adapt to sharp structure as can a
nonlinear method. We compare the methods in Monte Carlo simulation
and on two examples: phoneme classification based on log-periodograms
of spoken words, and the prediction based on psychometric data of a
post-traumatic stress disorder diagnostic test score.Keywords: pattern regression, adaptive splines, cubic spline regression, ridge regression, partial least squares.