In 1936 R.A. Fisher asked the pointed question, ``Has Mendel's Work
Been Rediscovered?'' The query was intended to open for discussion
whether someone altered the data in Gregor Mendel's classic 1866
research report on the garden pea, ``Experiments in
Plant-Hybridization.'' Fisher concluded, reluctantly, that the
statistical counts in Mendel's paper were doctored in order to create
a better intuitive fit between Mendelian expected values and observed
frequencies. That verdict remains the received view at least among
statisticians, so I believe.
Fisher's analysis is a tour de force of so-called ``Goodness of Fit''
statistical tests using 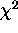 to calculate significance levels,
i.e., P-values. In this paper I attempt a defense of Mendel's report
based on several themes.
to calculate significance levels,
i.e., P-values. In this paper I attempt a defense of Mendel's report
based on several themes.
- Mendel's experiments include some important sequential design
features that Fisher and (to my knowledge) others ignore. This is
relevant to Fisher's charge that, for one crucial experiment,
Mendel's protocol had approximately a 5% error of misclassifying
hybrids as pure dominants.
- Fisher uses particular statistical techniques of Meta-analysis
for pooling outcomes from different experiments. These methods are
subject to critical debate.
- I speculate on a small modification to Mendelian theory for the
model of self-fertilization of garden pea that offers some relief
from Fisher's harsh conclusion that, overall, Mendel's data are too
good to be true. This last idea is yet another try to find an
empirically plausible reason for thinking that Mendel's pea data
should reflect sub-binomial variability.
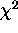 to calculate significance levels,
i.e., P-values. In this paper I attempt a defense of Mendel's report
based on several themes.
to calculate significance levels,
i.e., P-values. In this paper I attempt a defense of Mendel's report
based on several themes.
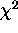 to calculate significance levels,
i.e., P-values. In this paper I attempt a defense of Mendel's report
based on several themes.
to calculate significance levels,
i.e., P-values. In this paper I attempt a defense of Mendel's report
based on several themes.