812

Efficient Estimation of Stochastic Volatility Using Noisy Observations: A Multi-Scale Approach

Lan Zhang

Revised 02/06

Abstract:

With the availability of high frequency financial data, nonparametric estimation of volatility of an asset return process becomes feasible. A major problem is how to estimate the volatility consistently and efficiently, when the observed asset returns contain error or noise, for example, in the form of microstructure noise. The former (consistency) has been addressed heavily in the recent literature, however, the resulting estimator is not quite efficient. In Zhang, Mykland, Ait-Sahalia (2003), the best estimator converges to the true volatility only at the rate of $n^{-1/6}$. 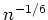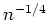In this paper, we propose an efficient estimator which converges to the true at the rate of $n^{-1/4}$, which is the best attainable. The estimator remains valid when the observation noise is dependent.

Here is the full PDF text for this technical report. It is 147425 bytes long.