, an unknown real-valued
parameter of interest. We assume that credible intervals are used to
establish whether belongs to an indifference region. This
problem is typical in clinical trials, where represents the
effect-difference of two alternative treatments and experiments are
judged conclusive only if one is able to exclude that
belongs to a range of equivalence. Following a robust Bayesian
approach, we model uncertainty on prior specification by a class
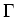
of distributions for and we assume that the data
yield robust evidence if, as the prior varies in ,
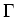
either the lower bound of the inferior limit of the credible set is
sufficiently large or the upper bound of the superior limit is
sufficiently small. Sample size determination criteria proposed in
the article consist in selecting the minimal number of observations
such that the experiment is likely to yield robust evidence. These
criteria require computations of summaries of the predictive
distributions of upper and lower bounds of the random limits of
credible intervals. The method is developed assuming a normal mean
as the parameter of interest and using conjugate priors. An
application to the determination of sample size for a trial of
surgery for gastric cancer is also illustrated. Keywords: Bayesian power, Bayesian robustness, clinical trials, evidence, predictive analysis, sample size determination, superiority trials