847

Adaptive Confidence Bands

Christopher Genovese and Larry Wasserman

Abstract:

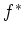
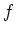
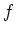
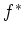
We show that there do not exist adaptive confidence bands for curve estimation except under very restrictive assumptions. We propose instead to construct adaptive bands that cover a surrogate function $f^*$ which is close to, but simpler than, $f$. The surrogate captures the significant features in $f$. We establish lower bounds on the width for any confidence band for $f^*$ and construct a procedure that comes within a small constant factor of attaining the lower bound for finite-samples.

Here is the full PDF text for this technical report. It is 358572 bytes long.