STAT3002 Week 1
1. Simple Linear Regression
Auction Data. The data give the selling
price (£) at auction of 32 antique grandfather clocks. Also recorded is the age
of the clock (in years) and the number of people who participated in the
bidding.
|
Age |
Bidders |
Price |
Age |
Bidders |
Price |
|
127 |
13 |
1235 |
170 |
14 |
2131 |
|
115 |
12 |
1080 |
182 |
8 |
1550 |
|
127 |
7 |
845 |
162 |
11 |
1884 |
|
184 |
10 |
2041 |
|||
|
156 |
6 |
1047 |
143 |
6 |
854 |
|
182 |
11 |
1979 |
159 |
9 |
1483 |
|
156 |
12 |
1822 |
108 |
14 |
1055 |
|
132 |
10 |
1253 |
175 |
8 |
1545 |
|
137 |
9 |
1297 |
108 |
6 |
729 |
|
113 |
9 |
946 |
179 |
9 |
1792 |
|
137 |
15 |
1713 |
111 |
15 |
1175 |
|
117 |
11 |
1024 |
187 |
8 |
1593 |
|
137 |
8 |
1147 |
111 |
7 |
785 |
|
153 |
6 |
1092 |
115 |
7 |
744 |
|
117 |
13 |
1152 |
194 |
5 |
1356 |
|
126 |
10 |
1336 |
168 |
7 |
1262 |
>
auction <- read.table("clipboard", header=T)
>
attach(auction)
>
price.lm <- lm(Price ~ Age)
>
summary(price.lm)
Call:
lm(formula = Price ~ Age)
Residuals:
Min
1Q Median 3Q Max
-485.3 -192.7 30.75 157.2 541.2
Coefficients:
Value Std. Error t value
Pr(>|t|)
(Intercept)
-191.6576 263.8866 -0.7263
0.4733
Age
10.4791 1.7900 5.8543
0.0000
Residual
standard error: 273 on 30 degrees of freedom
Multiple
R-Squared: 0.5332
F-statistic:
34.27 on 1 and 30 degrees of freedom, the p-value is 2.096e-006
Correlation
of Coefficients:
(Intercept)
Age
-0.9831
>
anova(price.lm)
Analysis
of Variance Table
Response:
Price
Terms
added sequentially (first to last)
Df Sum of Sq Mean Sq F Value Pr(F)
Age
1 2554859 2554859 34.27293
2.096498e-006
Residuals
30 2236335 74545
> names(price.lm)
[1] "coefficients"
"residuals"
"fitted.values" "effects"
[5] "R"
"rank"
"assign"
"df.residual"
[9] "contrasts"
"terms"
"call"
> price.lm$coefficients
(Intercept) Age
-191.6576 10.47909
> price.lm$df.residual
[1] 30
> win.graph(10,5)
> par(mfrow=c(1,2))
> plot(Age,Price)
> abline(price.lm)
>
plot(fitted(price.lm),residuals(price.lm))
> abline(0,0)

1.2
Confidence and Prediction Intervals
> newdata <-
list(Age=120)
> f <-
predict(price.lm,newdata,se.fit=T)
> f
$fit:
1
1065.834
$se.fit:
1
65.74217
$residual.scale:
[1] 273.0284
$df:
[1] 30
> f <-
predict(price.lm,se.fit=T)
> ci <- pointwise(f,coverage=0.90)
> ord <- order(Age)
>
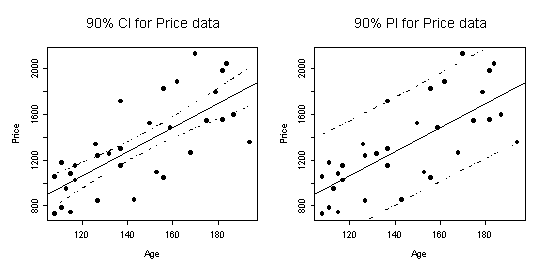
plot(Age,Price,main="90% CI for Price data")
> abline(price.lm)
>
lines(Age[ord],ci$upper[ord],lty=3)
>
lines(Age[ord],ci$lower[ord],lty=3)
> se.pred <-
sqrt(f$residual.scale^2 + f$se.fit^2)
> pi.upper <- f$fit +
qt(0.95,f$df)*se.pred
> pi.lower <- f$fit
+ qt(0.05,f$df)*se.pred
>
plot(Age,Price,main="90% PI for Price data")
> abline(price.lm)
>
lines(Age[ord],pi.upper[ord],lty=3)
>
lines(Age[ord],pi.lower[ord],lty=3)