STAT3002 Week 5

5. Variable Selection

Variable selection is the process where we try to find the best subset of x variables to predict the response y. In this section we shall examine four methods of variable selection.

> attach(costovr)

> LogItems <- log(Items) # log transformation

> Target03 <- Target^0.3 # power transformation

> par(mfrow=c(3,3))

> hist(Ceiling)

> hist(Contracts)

> hist(LogItems))

> hist(Months)

> hist(Price) # note low outlier

> hist(Share)

> hist(Target03)

> hist(Year)

> hist(Deviation) # appears reasonably symmetric

> par(mfrow=c(1,1))

> pairs(cbind(Ceiling,Contracts,LogItems,Months,Price,Share, Target03,Year,Deviation))

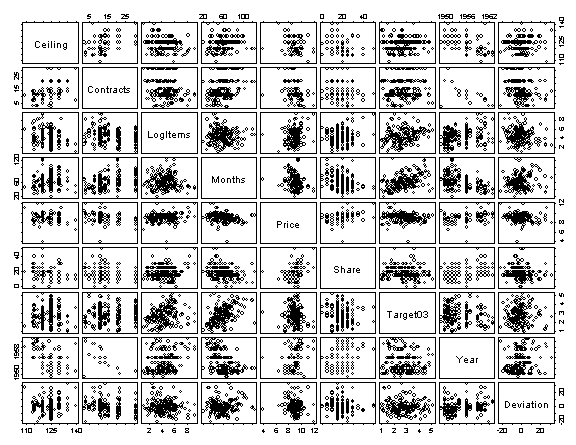
> xvar <- data.frame(Ceiling,Contracts,LogItems,Months,Price,Sharing,Target03,Year,Deviation)

5.1 Backward Elimination

> summary(lm(Deviation~.,data=xvar),cor=F)

Call: lm(formula = Deviation ~ ., data = xvar)

Residuals:

Min 1Q Median 3Q Max

-22.82 -4.278 -0.5248 3.445 31.09

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) -1813.7359 566.5246 -3.2015 0.0016

Ceiling 0.3931 0.1393 2.8227 0.0053

Contracts -0.2848 0.1169 -2.4353 0.0159

LogItems -0.5232 0.4311 -1.2137 0.2266

Months 0.1526 0.0411 3.7103 0.0003

Price -1.6187 0.8111 -1.9956 0.0476

Share -0.0881 0.0826 -1.0674 0.2873

Target03 -1.5213 0.8002 -1.9011 0.0590

Year 0.9121 0.2863 3.1859 0.0017

Residual standard error: 7.993 on 168 degrees of freedom

Multiple R-Squared: 0.2591

F-statistic: 7.346 on 8 and 168 degrees of freedom, the p-value is 2.333e-008

We could remove both LogItems and Share but we do not know if we can take them both out as they may be highly correlated. We can check the pairs plot for a rough idea, to see if they are highly correlated.

> summary(lm(Deviation~.-Share,data=xvar),cor=F)

Call: lm(formula = Deviation ~ . - Share, data = xvar)

Residuals:

Min 1Q Median 3Q Max

-22.41 -4.495 -0.527 3.529 31.97

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) -1716.4990 559.3824 -3.0686 0.0025

Ceiling 0.4031 0.1390 2.9002 0.0042

Contracts -0.3077 0.1150 -2.6756 0.0082

LogItems -0.5653 0.4295 -1.3164 0.1898

Months 0.1571 0.0409 3.8381 0.0002

Price -1.8202 0.7892 -2.3065 0.0223

Target03 -1.4399 0.7969 -1.8069 0.0726

Year 0.8618 0.2825 3.0506 0.0027

Residual standard error: 7.996 on 169 degrees of freedom

Multiple R-Squared: 0.2541

F-statistic: 8.225 on 7 and 169 degrees of freedom, the p-value is 1.283e-008

Continuing to the 1% significance level, our final model contains the predictors Ceiling, Months and Year.

> summary(lm(Deviation~.-Share-LogItems-Target03-Price-Contracts,data=xvar),cor=F)

Call: lm(formula = Deviation ~ . - Share - LogItems - Target03 - Price - Contracts, data = xvar)

Residuals:

Min 1Q Median 3Q Max

-24.23 -4.554 -0.5442 3.352 29.21

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) -2454.8597 424.9565 -5.7767 0.0000

Ceiling 0.4607 0.1411 3.2643 0.0013

Months 0.1258 0.0366 3.4330 0.0007

Year 1.2226 0.2130 5.7409 0.0000

Residual standard error: 8.326 on 173 degrees of freedom

Multiple R-Squared: 0.1722

F-statistic: 12 on 3 and 173 degrees of freedom, the p-value is 3.57e-007

Recall that the ‘Share’ variable is the variable the Economists argue will distinguish between contractors. Putting Share back into the model gives:

> summary(lm(Deviation~.-LogItems-Target03-Price-Contracts,data=xvar),cor=F)

Call: lm(formula = Deviation ~ . - LogItems - Target03 - Price - Contracts, data = xvar)

Residuals:

Min 1Q Median 3Q Max

-24.11 -4.343 -0.6701 3.297 28.74

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) -2503.6028 422.9099 -5.9199 0.0000

Ceiling 0.4316 0.1411 3.0595 0.0026

Months 0.1129 0.0371 3.0448 0.0027

Share -0.1493 0.0813 -1.8357 0.0681

Year 1.2512 0.2121 5.8995 0.0000

Residual standard error: 8.269 on 172 degrees of freedom

Multiple R-Squared: 0.1881

F-statistic: 9.963 on 4 and 172 degrees of freedom, the p-value is 2.83e-007

5.2 Best Subset Regression

We shall consider all possible subsets of the x variables and evaluate them quickly.

Using “Leaps and Bounds” Algorithm

See Furnival and Wilson (1974), “Regression by leaps and bounds”, Technometrics, 16, pp 499-511.

> xvar <- xvar[,1:8]

> costovr.bs1 <- leaps(xvar,Deviation,nbest=1)

> costovr.bs1

$Cp:

[1] 36.695637 26.135284 18.715302 15.766273 11.752866 7.873674 8.139296 8.999996

$size:

[1] 2 3 4 5 6 7 8 9

$label:

[1] "Contracts"

[2] "Contracts,Price"

[3] "Ceiling,Months,Year"

[4] "Ceiling,Contracts,Months,Year"

[5] "Ceiling,Contracts,Months,Price,Year"

[6] "Ceiling,Contracts,Months,Price,Target03,Year"

[7] "Ceiling,Contracts,LogItems,Months,Price,Target03,Year"

[8] "Ceiling,Contracts,LogItems,Months,Price,Share,Target03,Year"

$which:

[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]

[1,] F T F F F F F F

[2,] F T F F T F F F

[3,] T F F T F F F T

[4,] T T F T F F F T

[5,] T T F T T F F T

[6,] T T F T T F T T

[7,] T T T T T F T T

[8,] T T T T T T T T

$int:

[1] T

> summary(lm(Deviation~Ceiling+Contracts+Months+Price+Target03+Year),cor=F)

Call: lm(formula = Deviation ~ Ceiling + Contracts + Months + Price + Target03 + Year)

Residuals:

Min 1Q Median 3Q Max

-21.27 -4.46 -0.4779 3.672 31.46

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) -1634.3454 557.0874 -2.9337 0.0038

Ceiling 0.4106 0.1392 2.9499 0.0036

Contracts -0.3138 0.1151 -2.7255 0.0071

Months 0.1630 0.0408 3.9965 0.0001

Price -2.0007 0.7789 -2.5688 0.0111

Target03 -1.8083 0.7477 -2.4185 0.0166

Year 0.8193 0.2813 2.9128 0.0041

Residual standard error: 8.013 on 170 degrees of freedom

Multiple R-Squared: 0.2465

F-statistic: 9.268 on 6 and 170 degrees of freedom, the p-value is 8.725e-009

Using Stepwise function

> costovr.bs2 <- stepwise(xvar,Deviation,method="exhaustive")

> costovr.bs2

$rss:

[1] 1.339604e+004 1.360726e+004 1.423883e+004 1.259365e+004 1.271667e+004 1.272858e+004 1.199187e+004 1.209627e+004

[9] 1.217119e+004 1.161961e+004 1.167364e+004 1.167571e+004 1.129155e+004 1.130179e+004 1.133969e+004 1.091597e+004

[17] 1.101391e+004 1.113507e+004 1.080517e+004 1.082650e+004 1.096328e+004 1.073239e+004 1.000000e+035 1.000000e+035

$size:

[1] 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 1 0

$which:

Ceiling Contracts LogItems Months Price Share Target03 Year

1(#1) F T F F F F F F

1(#2) F F F F F F F T

1(#3) F F F F T F F F

2(#1) F T F F T F F F

2(#2) T T F F F F F F

2(#3) F T F T F F F F

3(#1) T F F T F F F T

3(#2) F T F T T F F F

3(#3) T T F F T F F F

4(#1) T F T T F F F T

4(#2) T F F T F F T T

4(#3) T T F T F F F T

5(#1) T T F T T F F T

5(#2) T T T T F F F T

5(#3) T T F T F F T T

6(#1) T T F T T F T T

6(#2) T T T T T F F T

6(#3) T T F T F T T T

7(#1) T T T T T F T T

7(#2) T T F T T T T T

7(#3) T T T T T T F T

8(#1) T T T T T T T T

1(#2) F F F F F F F T

0(#3) F F F F F F F F

$method:

[1] "exhaustive"

Computing C_p.

> sigma <- costovr.bs2$rss[22]/168

> p <- costovr.bs2$size+1

> n <- 177

> Cp <- costovr.bs2$rss/sigma + 2*p -n

> Syy <- sum((Deviation-mean(Deviation))^2)

> R2 <- 1 - costovr.bs2$rss/Syy

> sigmap <- sqrt(costovr.bs2$rss/(n-p))

> all.subsets <- data.frame(p,Cp,R2,sigmap)

> all.subsets <- all.subsets[Cp<1e30,]

> round(all.subsets,3)

p Cp R2 sigmap

1 2 36.696 0.075 8.749

2 2 40.002 0.061 8.818

3 2 49.888 0.017 9.020

4 3 26.135 0.131 8.507

5 3 28.061 0.122 8.549

6 3 28.248 0.121 8.553

7 4 18.715 0.172 8.326

8 4 20.350 0.165 8.362

9 4 21.522 0.160 8.388

10 5 14.888 0.198 8.219

11 5 15.734 0.194 8.238

12 5 15.766 0.194 8.239

13 6 11.753 0.221 8.126

14 6 11.913 0.220 8.130

15 6 12.506 0.217 8.143

16 7 7.874 0.246 8.013

17 7 9.407 0.240 8.049

18 7 11.303 0.231 8.093

19 8 8.139 0.254 7.996

20 8 8.473 0.253 8.004

21 8 10.614 0.243 8.054

22 9 9.000 0.259 7.993

5.3 Forward Selection

Forward selection can be done using either the stepwise() or add1() functions. We will do it the long way, using add1().

> costovr.fs0 <- lm(Deviation~1)

> add1(costovr.fs0,.~.+Ceiling+Contracts+LogItems+Months+Price+Share+Target03+Year)

Single term additions

Model:

Deviation ~ 1

Df Sum of Sq RSS Cp

<none> 14486.50 14651.11

Ceiling 1 99.308 14387.19 14716.43

Contracts 1 1090.452 13396.04 13725.28

LogItems 1 148.035 14338.46 14667.70

Months 1 161.706 14324.79 14654.03

Price 1 247.665 14238.83 14568.07

Share 1 243.842 14242.65 14571.89

Target03 1 10.581 14475.91 14805.15

Year 1 879.234 13607.26 13936.50

> costovr.fs1 <- lm(Deviation~Contracts,data=xvar)

> summary(costovr.fs1,cor=F)

Call: lm(formula = Deviation ~ Contracts, data = xvar)

Residuals:

Min 1Q Median 3Q Max

-25.09 -4.933 -1.097 3.867 32.49

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) 3.8895 1.4930 2.6051 0.0100

Contracts -0.2986 0.0791 -3.7743 0.0002

Residual standard error: 8.749 on 175 degrees of freedom

Multiple R-Squared: 0.07527

F-statistic: 14.25 on 1 and 175 degrees of freedom, the p-value is 0.0002195

> add1(costovr.fs1,.~.+Ceiling+LogItems+Months+Price+Share+Target03+Year)

Single term additions

Model:

Deviation ~ Contracts

Df Sum of Sq RSS Cp

<none> 13396.04 13702.24

Ceiling 1 679.3681 12716.67 13175.97

LogItems 1 335.7067 13060.34 13519.63

Months 1 667.4598 12728.58 13187.88

Price 1 802.3963 12593.65 13052.94

Share 1 368.6761 13027.37 13486.66

Target03 1 2.2263 13393.82 13853.11

Year 1 45.8213 13350.22 13809.51

> costovr.fs2 <- lm(Deviation~Contracts+Price,data=xvar)

> summary(costovr.fs2,cor=F)

Call: lm(formula = Deviation ~ Contracts + Price, data = xvar)

Residuals:

Min 1Q Median 3Q Max

-19 -5.271 -0.9265 4.029 31.1

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) 29.3800 7.7921 3.7705 0.0002

Contracts -0.3889 0.0816 -4.7677 0.0000

Price -2.6665 0.8008 -3.3296 0.0011

Residual standard error: 8.507 on 174 degrees of freedom

Multiple R-Squared: 0.1307

F-statistic: 13.08 on 2 and 174 degrees of freedom, the p-value is 5.121e-006

> add1(costovr.fs2,.~.+Ceiling+LogItems+Months+Share+Target03+Year)

Single term additions

Model:

Deviation ~ Contracts + Price

Df Sum of Sq RSS Cp

<none> 12593.65 13027.91

Ceiling 1 422.4574 12171.19 12750.21

LogItems 1 202.0002 12391.65 12970.66

Months 1 497.3784 12096.27 12675.29

Share 1 133.1216 12460.52 13039.54

Target03 1 21.8221 12571.82 13150.84

Year 1 60.5533 12533.09 13112.11

> costovr.fs3 <- lm(Deviation~Contracts+Price+Months,data=xvar)

> summary(costovr.fs3,cor=F)

Call: lm(formula = Deviation ~ Contracts + Price + Months, data = xvar)

Residuals:

Min 1Q Median 3Q Max

-18.68 -5.062 -1.099 4.222 31.48

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) 22.3176 8.1036 2.7540 0.0065

Contracts -0.4550 0.0839 -5.4223 0.0000

Price -2.3878 0.7940 -3.0072 0.0030

Months 0.0938 0.0352 2.6671 0.0084

Residual standard error: 8.362 on 173 degrees of freedom

Multiple R-Squared: 0.165

F-statistic: 11.39 on 3 and 173 degrees of freedom, the p-value is 7.407e-007

> add1(costovr.fs3,.~.+Ceiling+LogItems+Share+Target03+Year)

Single term additions

Model:

Deviation ~ Contracts + Price + Months

Df Sum of Sq RSS Cp

<none> 12096.27 12655.63

Ceiling 1 335.8458 11760.42 12459.63

LogItems 1 222.3423 11873.93 12573.13

Share 1 42.7484 12053.52 12752.73

Target03 1 317.5292 11778.74 12477.95

Year 1 244.7626 11851.51 12550.71

> costovr.fs4 <- lm(Deviation~Contracts+Price+Months+Ceiling,data=xvar)

> summary(costovr.fs4,cor=F)

Call: lm(formula = Deviation ~ Contracts + Price + Months + Ceiling, data = xvar)

Residuals:

Min 1Q Median 3Q Max

-17.89 -4.912 -0.8136 4.33 34.59

Coefficients:

Value Std. Error t value Pr(>|t|)

(Intercept) -16.9564 19.4484 -0.8719 0.3845

Contracts -0.5146 0.0872 -5.8994 0.0000

Price -2.0377 0.8009 -2.5441 0.0118

Months 0.0857 0.0350 2.4510 0.0152

Ceiling 0.3055 0.1379 2.2163 0.0280

Residual standard error: 8.269 on 172 degrees of freedom

Multiple R-Squared: 0.1882

F-statistic: 9.967 on 4 and 172 degrees of freedom, the p-value is 2.81e-007

We stop after this step, as there are no more useful predictors to be added.

5.4 Stepwise Regression

Stepwise regression may be done using either the stepwise() or step() command. We will do it using the stepwise() function.

> costovr.sw <- stepwise(xvar,Deviation)

> costovr.sw

$rss:

[1] 13396.04 12593.65 12096.27 11760.42 11291.55 10915.97

$size:

[1] 1 2 3 4 5 6

$which:

Ceiling Contracts LogItems Months Price Share Target03 Year

1(+2) F T F F F F F F

2(+5) F T F F T F F F

3(+4) F T F T T F F F

4(+1) T T F T T F F F

5(+8) T T F T T F F T

6(+7) T T F T T F T T

$f.stat:

[1] 14.245189 11.086301 7.113471 4.911854 7.100636 5.849138

$method:

[1] "efroymson"