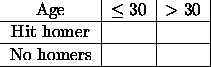
A zero in a contingency table can mean at least two different things.
It is easy to give examples of both types. If we did a two-way classification of professional baseball players by
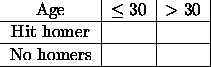
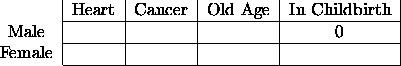
For an example of a fixed, or structural zero, consider the following cross-classification of causes of death. There is one cell which obviously (at least to me) must be empty.
The two types of zeros give rise to different problems. If there are too many sampling zeroes, it is possible that the maximum likelihood estimates for a model may not exist. The problem is that there is not enough information to estimate the model. There is a theorem to make this precise.
Structural zeroes (i.e., fixed in advance) do not in themselves cause
any estimation difficulties, but they may make it difficult to
formulate a model.
Reconsider the Sex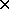 
Death table and view both variables as
responses. Lets make our initial model one that asks if cause of death
is independent of sec. This implies that the table of fitted values
must be
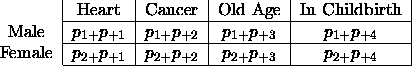
If the upper-right cell is non-zero, then we KNOW that there is something wrong.
Clearly we need to develop new models for this situation. One solution to this (particular) problem is to use the model of quasi-independence.
Let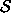 
be the set of cells which are net structural
zeros.
(E.g., above,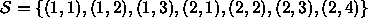 
. The
quasi-independence model would posit that
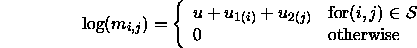
This ensures that the structural zeroes ``stay'' zero and the rest of the table displays an independence-like structure.
There are rarely closed-form estiamtes for these models, but they are easy to fit. Just add weights to the glm that weight the missing cell as zero and the other cells as one.
As an example, consider the following data. A colony of 6 monkeys was studied over a period of time and a record was kept of how often each monkey displayed its genitals toward each other monkey. The constraint is that monkeys cannot (at least in this experiment) display to themselves. The data appear below. Displayers
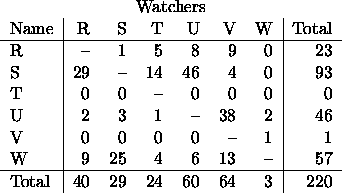
Notice that T is bashful and never displays---hence we really need to treat the entire 3rd row as well as the diagonal as structural zeros.
Now lets try to fit the quasi-independence model to these data.
402 > monkey <- fac.design(c(6,6),list(Watch=c("R","S","T","U","V","W"),
+ Display=c("R","S","T","U","V","W")))
402 > monkey$Resp <- scan("monkey.dat")
402 > monkey
Watch Display Resp
1 R R 0
2 S R 1
3 T R 5
4 U R 8
5 V R 9
6 W R 0
7 R S 29
8 S S 0
9 T S 14
10 U S 46
11 V S 4
12 W S 0
13 R T 0
14 S T 0
.........
Now set up the weights,
402 > wei <- rep(1,length(Resp)) 402 > monkey[Display=="T",] Watch Display Resp 13 R T 0 14 S T 0 15 T T 0 16 U T 0 17 V T 0 18 W T 0 402 > monkey[Display==Watch,] Watch Display Resp 1 R R 0 8 S S 0 15 T T 0 22 U U 0 29 V V 0 36 W W 0 402 > wei[Display=="T"] <- 0 402 > wei[Display==Watch] <- 0 402 > wei 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 0 1 1 1 1 1 1 0 1 1 1 1 0 0 0 0 0 0 1 1 1 0 1 1 1 1 1 1 0 30 31 32 33 34 35 36 1 1 1 1 1 1 0
Now, try to fit the model
402 > mymod <- glm(Resp ~ Watch + Display, family=poisson, weight=wei)
402 > anova(mymod)
Analysis of Deviance Table
Poisson model
Response: Resp
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 35 352.9142
Watch 16 95.6390 19 257.2753
Display 4 122.1061 15 135.1691
This clearly fits very poorly, the residuals and fitted values provide some insight.
402 > data.frame(Display, Watch, Resp, fitted(mymod), residuals(mymod)) Display Watch Resp fitted.mymod. residuals.mymod. 1 R R 0 4.61117003 0.00000000 2 R S 1 5.25950848 -2.28011881 3 R T 5 2.48072581 1.40368049 4 R U 8 8.21594826 -0.07567288 5 R V 9 6.64804865 0.86505430 6 R W 0 0.39577027 -0.88968564 7 S R 29 19.18599258 2.08150826 8 S S 0 21.88357619 0.00000000 9 S T 14 10.32171588 1.08537395 10 S U 46 34.18462584 1.91855873 11 S V 4 27.66096481 -5.64376708 12 S W 0 1.64670687 -1.81477650 13 T R 0 394.66861611 0.00000000 14 T S 0 450.15970329 0.00000000 15 T T 0 212.32455423 0.00000000 16 T U 0 703.20046854 0.00000000 17 T V 0 569.00442629 0.00000000 18 T W 0 33.87385456 0.00000000 19 U R 2 10.93639583 -3.32821201 20 U S 3 12.47407192 -3.22457813 21 U T 1 5.88358252 -2.49456075 22 U U 0 19.48591390 0.00000000 23 U V 38 15.76729789 4.73158037 24 U W 2 0.93865554 0.95032975 25 V R 0 0.22001588 -0.66334890 26 V S 0 0.25095050 -0.70844971 27 V T 0 0.11836455 -0.48654816 28 V U 0 0.39201311 -0.88545256 29 V V 0 0.31720286 0.00000000 30 V W 1 0.01888366 2.44472583 31 W R 9 9.65764532 -0.21409227 32 W S 25 11.01552689 3.60687599 33 W T 4 5.19563795 -0.54687791 34 W U 6 17.20750128 -3.12601524 35 W V 13 13.92368867 -0.25035727 36 W W 0 0.82890217 0.00000000
It appears that the Display is directed toward specific members (not randomly).