 is a log-linear model with all possible main effects and
interactions, and each model in the table differs from the one above
it by deleting one or more parameters.
is a log-linear model with all possible main effects and
interactions, and each model in the table differs from the one above
it by deleting one or more parameters.
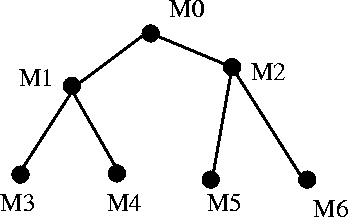
In order to select a model it is necessary that we be able to
compare models. Consider the following schematic situation, where
 is a log-linear model with all possible main effects and
interactions, and each model in the table differs from the one above
it by deleting one or more parameters.
is a log-linear model with all possible main effects and
interactions, and each model in the table differs from the one above
it by deleting one or more parameters.
Models  with
with 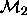 can be compared using either
Pearsons
can be compared using either
Pearsons 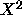 or the log-likelihood
or the log-likelihood 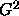 statistic. So can
models
statistic. So can
models 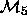 with
with 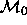 . For the
. For the 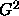 statistics
(and not the
statistics
(and not the 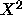 statistic) it is true that
statistic) it is true that
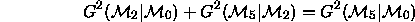
i.e., an additive partition of 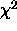 with the two components
being independent
with the two components
being independent 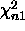 and
and 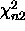 components.
components.
Thus, the techniques available allow us to compare, say, 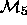 with
with 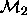 but that does not necessarily allow for a comparison
between
but that does not necessarily allow for a comparison
between 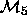 with
with 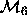 . This is exactly the
same problem we face in linear regression---where we looked at things
like RSS, residuals, and other properties to decide on a good model.
. This is exactly the
same problem we face in linear regression---where we looked at things
like RSS, residuals, and other properties to decide on a good model.
We will discuss formal selection techniques (like forward selection and backward elimination), and less formal, but more useful, techniques based on (conditional) independence diagrams. Often we will use our intuitions about the relationships between the factors to help constrain the models we are building.
Digression:
We say that 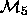 and
and 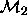 are nested
models, because the set of parameters in
are nested
models, because the set of parameters in 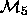 is a subset of
the parameters in
is a subset of
the parameters in 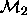 ; but
; but 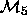 and
and 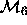 are
nonnested, since neither parameter set is a subset of the
other. All of our techniques for deciding between non-nested models
are informal; formal methods based on
are
nonnested, since neither parameter set is a subset of the
other. All of our techniques for deciding between non-nested models
are informal; formal methods based on 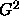 or
or 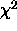 are valid only
for comparing nested models.
are valid only
for comparing nested models.
This inability to formally compare nonnested models is considered a weakness of standard statistical theory. A theory of statistics based on Bayes' Rule, called Bayesian Statistics, would allow us to make formal comparisons of non-nested models, using a weighted version of likelihood ratio tests called ``Bayes factors''. We would pay for this added flexibility by having to make additional modeling assumptions, for example, we would have to attach a ``prior'' distribution describing where we thought the parameter values would lie, to each parameter in the model. Nevertheless, the Bayesian approach is mathematically and inferentially powerful, and unifies many ideas in statistics (for example, a simple and compelling analysis of the split-plot and mixed effects models that we considered in ANOVA could be given by embedding these models in a Bayesian framework.)