Finger Exercises --- Due Thursday January 29, 1998

Please prepare answers for these exercises, to be turned in. Your grade will be based on how many questions you made a reasonably strong effort to answer, not how many questions you get right or partially right. There is no partial credit, but the grader may give you additional written feedback on each question you attempt.

Feel free to discuss these exercises with each other and with me. You will get the most benefit from the grader's remarks, however, if the work you turn in is your own.

This hw, like most material for this course, is posted on the World Wide Web at URL http://www.stat.cmu.edu/~brian/402/ ; you can cut and paste data directly out of the TeX file if you wish. Look for something under week2.

The first two questions are ``reviews'' of your previous work in Statistics and of your common sense, calculus skill, etc. The remaining questions are about ANOVA.

Box, Hunter and Hunter, p. 155. Every 90 minutes, routine readings are made of the level of asbestos fiber present in the air at an industrial plant. A salesman claimed that spraying with a chemical, S-424, could be beneficial. Arrangements were made for a comparative trial in the plant itself. Four consecutive readings, the first two without S-424 and the second two with S-424, were as follows:

In light of past data collected without the chemical spray, given below, do you think the additive works?

                  Asbestos Levels (112 consecutive readings)
        Dec  6    9 10  9  8  9  8  8  8  7  6  9 10 11  9 10 11
        Dec  7   11 11 11 10 11 12 13 12 13 12 14 15 14 12 13 13 
        Dec  8   12 13 13 13 13 13 10  8  9  8  6  7  7  6  5  6
        Dec  9    5  6  4  5  4  4  2  4  5  4  5  6  5  5  6  5
        Dec 10    6  7  8  8  8  7  9 10  9 10  9  8  9  8  7  7
        Dec 11    8  7  7  7  8  8  8  8  7  6  5  6  5  6  7  6
        Dec 12    6  5  6  6  5  4  3  4  5  5  6  5  6  7  6  5

Explain and justify your answer, using both statistical and nonstatistical means. Explicitly state all assumptions you are making about the problem. Do not worry about whether or not your answer involves regression, ANOVA, or any other particular method; just do the right things.

Box, Hunter and Hunter, p. 158. An agricultural engineer is trying to develop a special piece of equipment for processing a crop immediately after harvesting. Two configurations of this equipment are to be compared. Twenty runs are to be performed during a period of five days. Each run involves setting up the equipment in either configuration I or configuration II, harvesting a given amount of crop, processing it on the equipment, obtaining a quantitative measure of performance, and cleaning the equipment. Since there is only one piece of equipment, the tests must be done one at a time. The engineer has asked you to consult on this problem.

1. What questions would you ask him?
2. What advice might you give him about planning the experiment?
3. The engineer believes that a most accurate experiment requires an equal number of runs to be performed with each configuration. What assumptions would make it possible to demonstrate in a quantitative way that this is true?

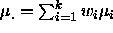In the ``grand mean plus effects'' model of lecture from Thursday Jan 22, suppose that we define in terms of the cell means 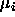, where 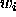are positive constants such that 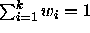. If we now define the treatment effects to be 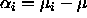, show that

Please

do some analysis for both questions 4 and 5, but only write up one of them.

Questionnaire color. [Neter, Wasserman and Kutner, 1990, pp. 562--563.] In an experiment to investigate the effect of color of paper (blue, green, orange) on response rates for questionnaires distributed by the ``windshield method'' in supermarket parking lots, 15 representative supermarket parking lots were chosen in a metropolitan area, and each color was assigned at random to five of the lots. The response rates, in percents, are listed in the table below.

  BLUE 28 26 31 27 35
 GREEN 34 29 25 31 29
ORANGE 31 25 27 29 28

1. Is this an experiment or an observational study? Explain.

2. Fit the one-way analysis of variance model; test the hypothesis the response rates vary depending on the color.

3. Do the data look like they satisfy the assumptions of the ANOVA / linear regression model? Inspect boxplots at each of the factor levels, fitted, residual and QQ plots, and use whatever other evidence you can think of to answer this question.

4. If you found evidence of unequal variances in the cells, nonnormality of residuals, or other problems, explain the problem(s) and try to fix them as best you can. If neccesary, re-run the ANOVA problem with the fixed dataset.

5. Obtain naive (that is, not adjusted for multiple comparisons) confidence intervals for each of the following:
   • The cell means in the cell means model ;
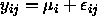   • The treatment (factor level) effects in the grand mean plus effects model , with the constraint that .

6. When informed of the findings, an executive said, ``See? I was right all along. We might as well print the questionnaires on plain white paper, which is cheaper!'' Does this conclusion follow from the findings of the study? Discuss.

Rehabilitation therapy. [Neter, Wasserman and Kutner, 1990, pp. 562--563.] A rehabilitation center researcher was interested in examining the relationship between physical fitness prior to persons undergoing corrective knee surgery and time required in physical therapy until successful rehabilitation. Patient records in the rehabilitation center were examined, and 24 make subjects ranging in age from 18 to 34 years who had undergone similar corrective knee surgery during the past year were selected for the study. The number of days required for successful completion of physical therapy, and the prior physical fitness status, are listed in the table below.

Fitness Score Nobs  1  2  3  4  5  6  7  8  9 10 
  BELOW    83    8 29 42 38 40 43 40 30 42      
AVERAGE   100   10 30 35 39 28 31 31 29 35 29 33
  ABOVE   121    6 26 32 21 20 23 22

In the table, ``Score'' is the mean score of men in each fitness group, on a standard medical fitness checklist (scores could range from 0 to 150), and ``Nobs'' is the number of observations in each fitness group.

1. Is this an experiment or an observational study? Explain.

2. Fit the one-way analysis of variance model; test the hypothesis 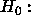the recovery (days needed in physical therapy) times vary depending on the prior fitness of the patient.

3. Do the data look like they satisfy the assumptions of the ANOVA / linear regression model? Inspect boxplots at each of the factor levels, fitted, residual and QQ plots, and use whatever other evidence you can think of to answer this question.

4. If you found evidence of unequal variances in the cells, nonnormality of residuals, or other problems, explain the problem(s) and try to fix them as best you can. If neccesary, re-run the ANOVA problem with the fixed dataset.

5. Estimate a 99% confidence interval for the mean recovery time (days in physical therapy) needed by someone of average fitness prior to the surgery.

6. Obtain confidence intervals for 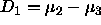and , using each of the three methods:
   • Bonferroni
   • Scheffé
   • Tukey
   Which method gives the best (shortest) intervals, in this case?

7. Now suppose you also want to compute an interval for 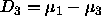. Which of the three procedures has to be recomputed? Why? Give the new interval(s) for any procedure(s) that need recomputing.

8. The scores 83, 100 and 121 were the average fitness scores in each fitness group. Can you say anything reasonable about the relationship between the numerical fitness score of a patient and the recovery time needed? Discuss.

• About this document ...