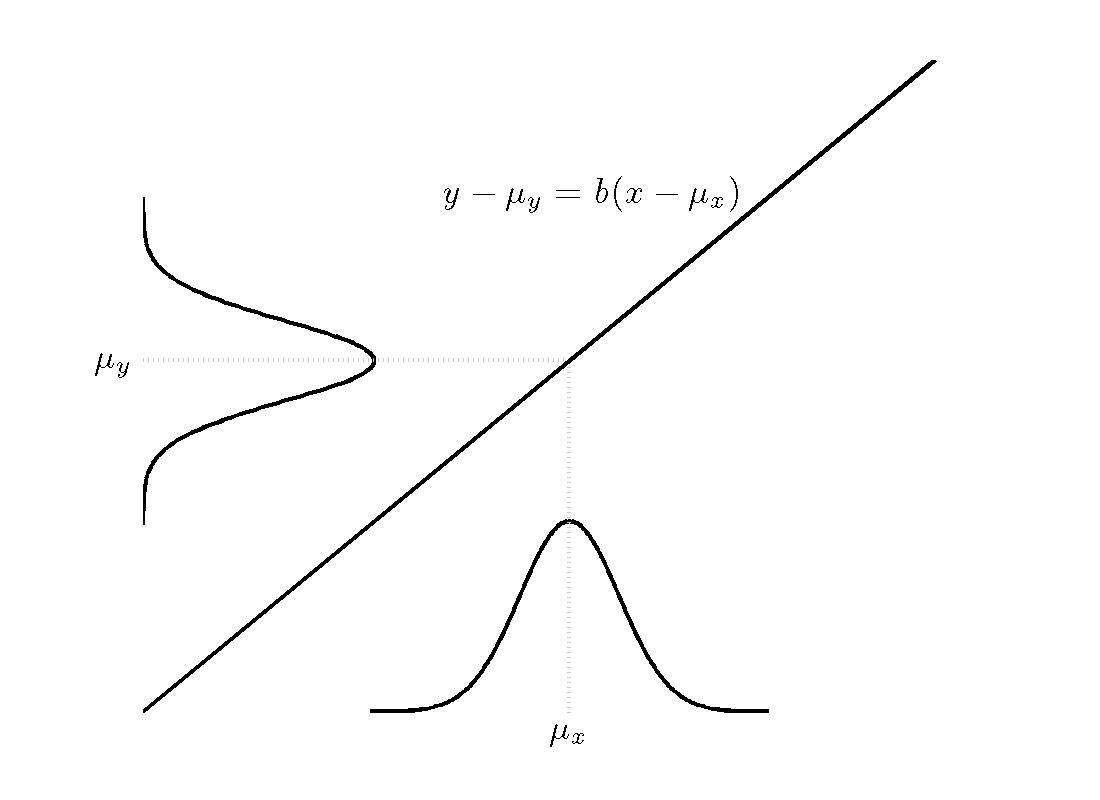
%
%
%  Figure caption:  The effect of the transformation y = a + bx
%  operating on a normally distributed random variable X having
%  mean muX and standard deviation sigmaX.  The random variable Y =
%  a + bX is again normally distributed, with mean muY = a + b*muX
%  and standard deviation sigmaY = |b| sigmaX.  The normal
%  distributions are displayed on the x and y axes; the linear
%  transformation is displayed as a line, which passes through the
%  point (muX, muY) so that it may be written, equivalently, as y -
%  muY = b(x - muX).

%  For Y = a + b*X,  we use a = 0, b = 0.7.  
a = 0; b = 0.7;

%  Set up normal random variable X.
xMu = 3; xSd = 0.35;

%  Set Y up as transformation of X. 
yMu = b*xMu+a;
ySd = abs(b)*xSd;

xMax = 2*xMu;            % Used for setting x-axes.  

%  Get a reasonable range of values to evaluate the PDF.
xValues = (xMu - 4*xSd) : 0.01 : (xMu + 4*xSd) ;
yValues = a + b * xValues;
xDensity = normpdf(xValues, xMu, xSd);
yDensity = normpdf(yValues, yMu, ySd);

%  Plot x first. 
plot(xValues, xDensity, 'k', 'LineWidth', 3)
hold on;
%  Add y.  
plot(yDensity, yValues, 'k', 'LineWidth', 3)

%  Add lines from the mean of x and y to where they meet.
line([xMu, xMu], [0, yMu], 'LineStyle', ':', ...
     'Color', [0.8, 0.8, 0.8], 'LineWidth', 3)
line([0, xMu], [yMu, yMu], 'LineStyle', ':', ...
     'Color', [0.8, 0.8, 0.8], 'LineWidth', 3)

%  Set figure style.  
text(2.1, 3.1, '$\it{y}-\mu_y = b(x-\mu_x)$', ...
     'FontSize', 22, 'Interpreter', 'LaTex')
set(gca, 'Box', 'off', ...
         'XLim', [0, xMax], 'YLim', [0, b*xMax+a], ...
         'XTick', [], 'YTick', [], ...
         'XColor', 'w', 'YColor', 'w')

transformationLine = refline(b, a);
set(transformationLine, 'Color', 'k', 'LineWidth', 3)
set(gca, 'Ylim', [0, b*xMax+a-0.3])

xlabel('$\it\mu_x$', 'FontSize', 22, 'Color', 'k', 'Interpreter', 'LaTex')
ylabel('$\it\mu_y$', 'FontSize', 22, 'Color', 'k', 'Interpreter', 'LaTex', ...
       'Rotation', 0)

xlabh = get(gca, 'XLabel');
ylabh = get(gca, 'YLabel');
set(xlabh, 'Position', [xMu, -0.07]);
set(ylabh, 'Position', [-0.2, 2]);

%  Close and set position.  
set(gcf, 'Position', [100, 100, 1100, 800])