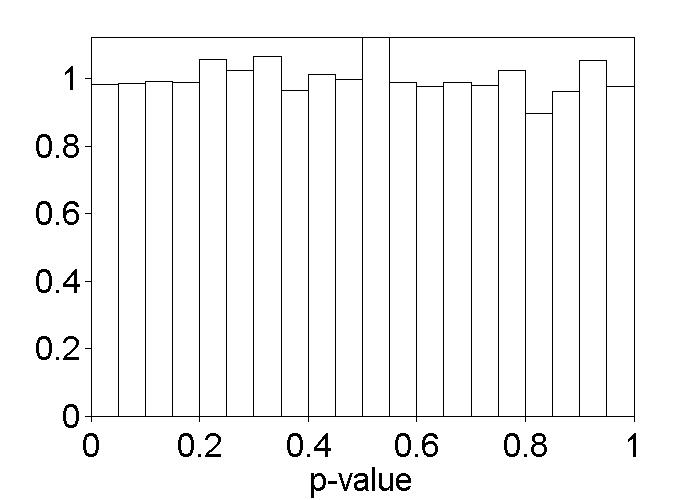
%
%
%  Figure caption:  Histogram of test-enhanced learning p-values
%  under H0.  Each p-value was computed by sampling at random the
%  60 data values under the SSSS and SSST conditions and
%  arbitrarily putting them into two groups of 30 each, then
%  running a t-test, as in the t-test on page 265.  This was
%  repeated 10,000 times.  The histogram was normalized by dividing
%  the number of observed p-values, in each bin, by the number
%  expected if they followed a U(0,1) distribution.


drk = csvread('rk.csv');
nTestOutcomes = numel(drk)

alldrk = drk(:);    % Formats data into a vector. 
nPermutations = 10000;
pValues = zeros(nPermutations, 1);

for i = 1:nPermutations
    shuffledTestOutcomes = alldrk(randperm(nTestOutcomes));
    fakeSsssOutcomes = shuffledTestOutcomes(1:30, 1);
    fakeSsstOutcomes = shuffledTestOutcomes(31:60, 1);
    [h, pValue] = ttest(fakeSsssOutcomes, fakeSsstOutcomes);
    pValues(i, 1) = pValue;
end

%  Plot the histogram of observed p-values.
hist(pValues, 0.025:0.05:0.975)
set(gca, 'Box', 'off', 'FontSize', 20, ...
         'YLim', [0, 560], 'XTick', 0:0.2:1, 'YTick', [], 'TickDir', 'out')

%  Set faces to white.
meanhist = findobj(gca, 'Type', 'patch');
set(meanhist, 'FaceColor', 'w')

%  Add labels and set figure position.  
xlabel('p-value', 'FontSize', 20)
set(gcf, 'Position', [200, 100, 700, 500])


%%  The following will rescale the y axis (as in the book) if desired (with
%%  one at the true mean, rather than empirical)

axesPosition = get(gca,'Position');

%  The first sets a y-axis on the left, the second copies it on the
%  right.  
hNewAxes = axes('Position', axesPosition, 'Box', 'off', 'FontSize', 20, ...
                'Color', 'none', 'TickDir', 'out', ...
                'XAxisLocation', 'top', 'YAxisLocation', 'left', ...
                'YLim', [0, 1.12], 'XTick', [], 'YTick', 0:0.2:1);
hNewAxes = axes('Position', axesPosition, 'Box', 'off', 'FontSize', 20, ...
                'Color', 'none', 'TickDir', 'out', ...
                'XAxisLocation', 'top', 'YAxisLocation', 'right', ...
                'YLim', [0, 1.12], 'XTick', [], 'YTick', []);