#  This script fits a 20th order polynomial to noisy observations of 
#     f(x) = sin(x) + 2*exp( - 30 * x^2)
#
#
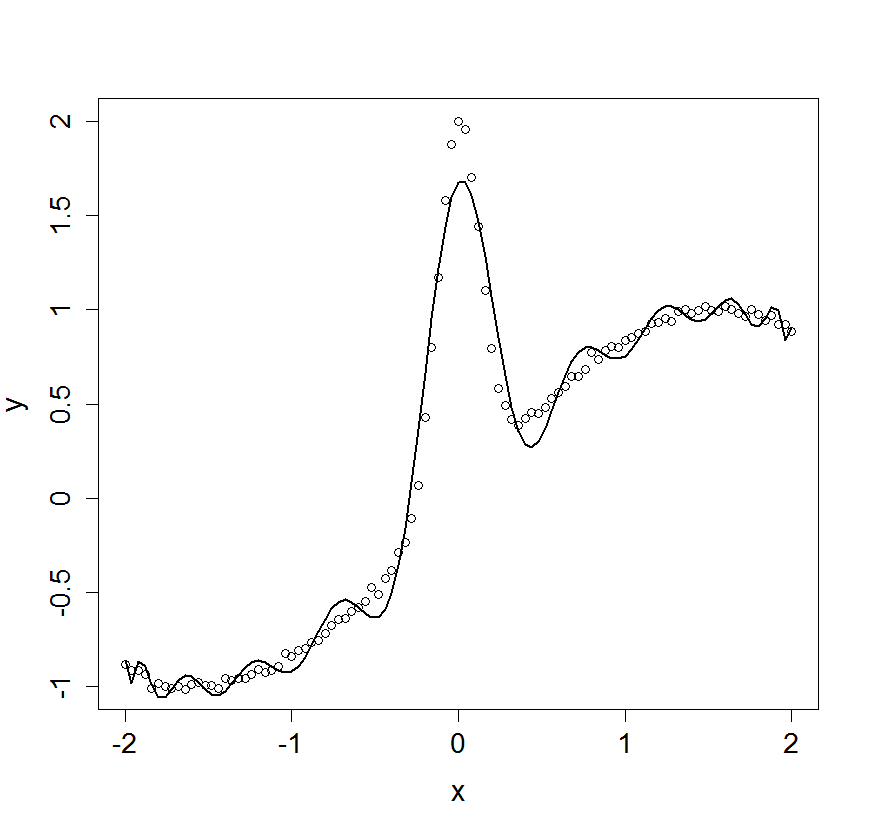
#  Figure caption:  Data simulated from function f(x) = sin(x) +
#  2exp(-30*x*x) together with twentieth order polynomial fit
#  (shown as line).  Note that the polynomial is over-fitting
#  (under-smoothing) in the relatively smooth regions of f(x), and
#  under-fitting (over-smoothing) in the peak.  (In the data shown
#  here, the noise standard deviation is 1/50 times the standard
#  deviation of the function values.)

n.observations <- 101
polynomial.order <- 20

#  Set up observations and function values.
x.at.obs <-seq(from = -2, to = 2, length.out = n.observations)
f.at.obs <- sin(x.at.obs) + 2*exp(-30 * (x.at.obs^2))

#  Obtain a reasonable noise level and add noise.  
f.sd <- sd(f.at.obs)
relative.noise <- 1/50
added.noise.sd <- f.sd * relative.noise
added.noise <- rnorm(n.observations, 0, added.noise.sd)
observations <- f.at.obs + added.noise

#  Obtain all polynomials.  
m.polynomials <- matrix(0, n.observations, polynomial.order)
for(i in 1:polynomial.order){
	m.polynomials[,i] <- x.at.obs^i
}


polynomial.model <- lm(observations ~ m.polynomials)
polynomial.predictions <- fitted(polynomial.model)

plot(x.at.obs, observations, 
     xlim = c(-2, 2), ylim = c(-1, 2), xaxt = "n", yaxt = "n", 
     main = "", xlab = "x", ylab = "y", cex.lab = 1.5)
lines(x.at.obs, polynomial.predictions, col = 153, lwd = 2)
points(x.at.obs, observations)
    
#  Clean up axes.
axis.size <- 1.4
x.axis <- seq(from = -2, to = 2, by = 1)
y.axis <- seq(from = -1, to = 2, by = 0.5)
axis(1, at = x.axis, labels = x.axis, cex.axis = axis.size)
axis(2, at = y.axis, labels = y.axis, cex.axis = axis.size)

#  Close the graphics device.  
dev.print(device = postscript, "15.2.added.noise", horizontal = TRUE)