# Script runs 1,000 simulations drawing a sample of size 100 from a
# Poisson distribution, and then plots histograms of the estimated
# means and estimated variances.
#
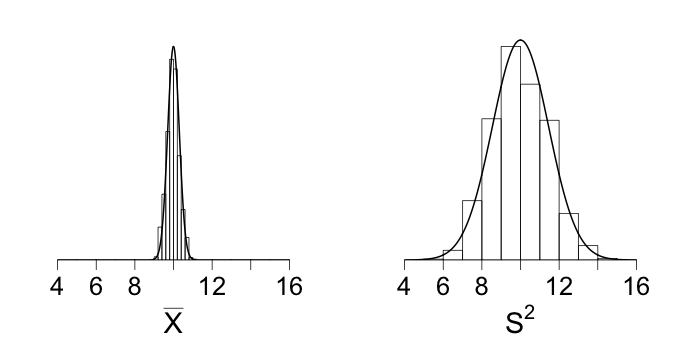
# Figure caption: Histograms displaying distributions of X-bar and S
# squared based on 1,000 randomly generated samples of size n = 100
# froma Poisson distribution with mean parameter mu = 10. In these
# repeated samples, both X-bat and S squared have distributions that
# are approximately normal. Both distributions are centered at 10
# (both estimators are unbiased) but the values of S squared
# fluctuate much more than do the values of X-bar.
nSimulations <- 1000
nSamples <- 100
lambda <- 10
# Generate all samples at once.
simulationSamples <- rpois( nSimulations * nSamples, lambda)
dim(simulationSamples) <- c( nSamples, nSimulations )
# Now that we have a matrix of poisson samples, with 1000 columns and
# 100 rows, each column can be considered a simulation.
sampleMeans <- apply(simulationSamples, 2, mean)
sampleVariances <- apply(simulationSamples, 2, var)
xValues<-seq(4, 16, by = 0.01)
par(mfrow = c(1, 2))
par(xaxs = "i")
par(yaxs = "i")
par(mar = c(5, 3, 1, 3))
# Plot the sample means histogram.
hist(sampleMeans, freq = FALSE,
xlim = c(4, 16), ylim = c(0, 1.5),
yaxt = "n", main = "", xlab = expression(bar(X)), ylab = "",
cex.lab = 1.8, cex.axis = 1.6)
# Add a line for the theoretical pdf of the sample mean.
# This is normal with mean lambda and variance
sampleMeansVariance = lambda / nSamples
lines(xValues, dnorm(xValues, lambda, sqrt(sampleMeansVariance)), lwd = 2)
# Plot the sample variances histogram.
hist(sampleVariances, freq = FALSE,
xlim = c(4, 16), ylim = c(0, 0.3),
yaxt = "n", main = "", xlab = expression(S^{2}), ylab = "",
cex.lab = 1.8, cex.axis = 1.6)
# Compute the variance of the sample variances and plot the
# theoretical density.
sampleVariancesVariance <- (lambda/nSamples) + 2 * (lambda^2 / (nSamples - 1))
theoreticalPdf <- dnorm(xValues, lambda, sqrt(sampleVariancesVariance))
lines(xValues, theoreticalPdf, lwd = 2)
# Print the figure as a postscript.
dev.print(device = postscript, "8.2.eps", horizontal = TRUE)