These may be obtained from my selected publications page.
About BARS
BARS (Bayesian Adaptive Regression Splines) solves the generalized nonparametric regression (curve-fitting) problem

A substantial literature has
demonstrated the power of spline-based generalized curve-fitting.
See Hansen and Kooperberg (2002, Statist. Science) for a review.
The difficult part of the problem is to allow aspects of the spline to
vary (adaptively to the data) across the domain of ![]() .
DiMatteo, Genovese, and Kass (2001, Biometrika) proposed BARS and
contributed an initial implementation and study of the method.
.
DiMatteo, Genovese, and Kass (2001, Biometrika) proposed BARS and
contributed an initial implementation and study of the method.
BARS
- assumes
- prior information about the
number of knots is formulated as a prior probability distribution (e.g.,
uniform on the integers from 1 to a maximal value
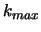 );
);
- prior information about the
number of knots is formulated as a prior probability distribution (e.g.,
uniform on the integers from 1 to a maximal value
- uses
- reversible-jump MCMC on the knot sets;
- Laplace's method, to integrate the spline coefficients;
- continuous proposals for knot locations, which attempt to place new knots near existing knots; and,
- in existing implementations, ``unit-information priors'' on the spline coefficients, given the knot set. (This is not essential to the method.)
- BARS computes
- a posterior distribution on the knot sets, and
- a posterior
distribution on any set of function values
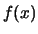 .
.
DiMatteo et al. compared BARS to two recently successful methods of solving the usual curve-fitting problem.
- Denison, Mallick, and Smith (DMS; JRSSB, 1998): a quasi-Bayesian
approach, which they found provided smaller MSE than wavelet
fits in examples from Donoho and Johnstone (1995).
- Zhou and Shen (SARS; JASA, 2001): an optimization method,
which they said
``performed at least as well as the spline competitors in all ...
examples, and significantly better in some,'' and again provided smaller MSE
than wavelet fits in examples from Donoho and Johnstone (1995).
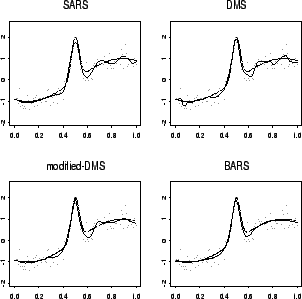
A typical data set simulated from a true curve, together with fits for each of DMS, SARS, and BARS are shown in the following figure. The fits are all a bit more wiggly than the true curve, but BARS provides a smoother fit while still capturing the sudden jump. Mean-squared errors in several examples were much smaller for BARS than for DMS or SARS.
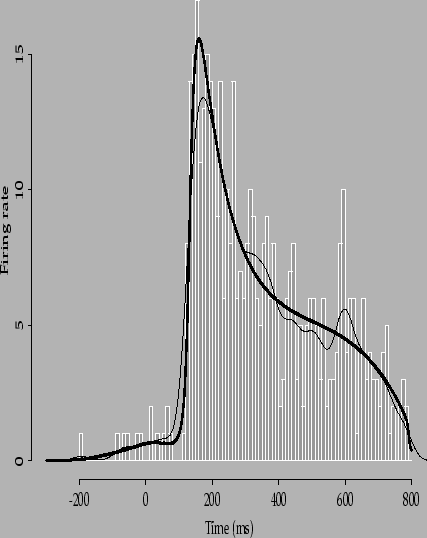
The next figure shows a BARS Poisson regression fit (thick curve) to neuronal data, providing the kind of smoothing we believe to be desirable; also shown is a Gaussian kernel density (Gaussian filter) estimate (thin curve). Taken from Kass, Ventura, Cai (2003, NETWORK: Computation in Neural Systems).