814

Finitely Additive Uniform Distributions on the Natural Numbers: Shift-Invariance

Oliver Schirokauer and Joseph B. Kadane

Updated: February 2006

Abstract:

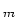
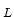
We compare the following three notions of uniformity for a finitely additive probability measure on the set of natural numbers: that it extend limiting relative frequency, that it be shift-invariant, and that it map every residue class mod $m$ to $1/m$. We find that these three types of uniformity can be naturally ordered. 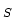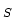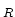In particular, we prove that the set $L$ of extensions of limiting relative frequency is a proper subset of the set $S$ of shift-invariant measures and that $S$ is a proper subset of the set $R$ of measures which map residue classes uniformly. 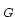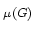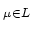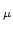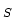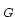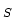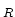Moreover, we show that there are subsets $G$ of $\enn$ for which the range of possible values $\mu(G)$ for $\mu\in L$ is properly contained in the set of values obtained when $\mu$ ranges over $S$, and that there are subsets $G$ which distinguish $S$ and $R$ analogously.

Keywords:imit points, limiting relative frequency, non-conglomerability, probability charge, residue class, shift-invariance

Here is the full PDF text for this technical report. It is 162870 bytes long.