860

On the $\ell_1-\ell_q$ Regularized Regression

Han Liu and Jian Zhang

Abstract:

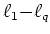
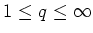
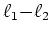
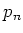
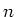
In this paper we consider the problem of grouped variable selection in high-dimensional regression using $\ell_1\text{-}\ell_q$ regularization ( $1\leq q \leq \infty$), which can be viewed as a natural generalization of the $\ell_1\text{-}\ell_2$ regularization (the group Lasso). The key condition is that the dimensionality $p_n$ can increase much faster than the sample size $n$, i.e. 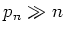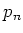$p_n \gg n$ (in our case $p_n$ is the number of groups), but the number of relevant groups is small. 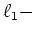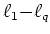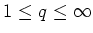The main conclusion is that many good properties from $\ell_1\text{-}$regularization (Lasso) naturally carry on to the $\ell_1\text{-}\ell_q$ cases ( $1\leq q \leq \infty$), even if the number of variables within each group also increases with the sample size. With fixed design, we show that the whole family of estimators are both estimation consistent and variable selection consistent under different conditions. We also show the persistency result with random design under a much weaker condition. 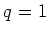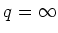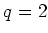These results provide a unified treatment for the whole family of estimators ranging from $q=1$ (Lasso) to $q=\infty$ (iCAP), with $q=2$ (group Lasso)as a special case. 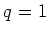When there is no group structure available, all the analysis reduces to the current results of the Lasso estimator ($q=1$).

Here is the full PDF text for this technical report. It is 259439 bytes long.