Next: Model Selection Example: Up: No Title Previous: Some Notation and

Graphical Models---An Aid for Higher Dimensional Tables

The Hierarchical Terms Rule ensures that our parameters will have nice interpretations, just as with ANOVA models: an interaction term fits the variation in the data that is not well-modeled by the corresponding lower-order terms. However this rule is not very helpful in building up a model.

For high dimensional tables (say 6 or higher) it is very difficult to develop models (let alone good models) without some form of extra guidance. A special case of hierarchical models, called graphical models allow one to draw useful pictures which can be a major help in selecting and interpreting models.

A graphical model is a hierarchical model (satisfies the Hierarchical Terms Rule above) that also satifies the following ``triangulation rule'':

Graphical Terms Rule: If A, B, and C are factors then the interactions A*B, A*C, and B*C imply that the A*B*C interaction must also be in the model.

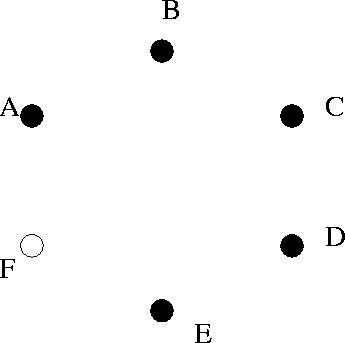
Consider a model with 6 factors ( A-- F). Draw 6 points. For each two-way interaction in the model, add a line joining the points. For each factor not included in the model, change the filled circle to an unfilled one.

As an example, the model A*B*C + C*D*E has the following picture.

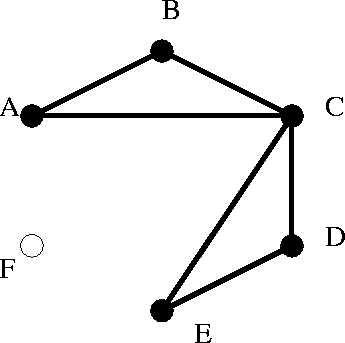
From the picture we can read off that D and E are independent of B and A given C.
Can we draw a picture of A*B*C + C*D*E + A*E?
A useful way to use these graphs is the choose models by adding and deleting edges to the graphs.
For example, -0.5in is A+B+C+D,

and -0.5in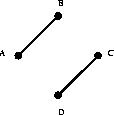 is A*B + C*D,

and -0.5in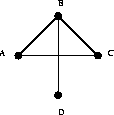 is A*B*D + C.
Notes:
Some hierarchical models, like A*B + B*D + A*D + C, are not graphical models, but they can be ``promoted'' to graphical models by triangulation. In this case, the terms A*B + B*D + A*D force us to add the term A*B*D, and then, deleting redundant terms, we are left with the graphical model A*B*D + C considered above.
Some models, like A*B + B*D + A*C express a conditional independence relationship (here, A and D are independent, given B and C) but cannot be represented well graphically.
If you know the time-order of the variables or you know other relationships between them, you can change the edges of a graph to arrows to indicate possible cause-and-effect relationships. For example in the graph for A*B*D + C, if we know that B occurs after all the other variables, we might change all the edges connecting A, C, and D to B into arrows pointing to B (and leave the edge between A and D alone, if there is no cause-and-effect hypothesis. Whether this makes sense depends on the problem context, presence or absence of unmeasured confounders, etc., of course!

Next: Model Selection Example: Up: No Title Previous: Some Notation and

Brian Junker
Thu Mar 12 08:42:49 EST 1998