 contingency
table where the classification variables are
contingency
table where the classification variables are
Consider the following  contingency
table where the classification variables are
contingency
table where the classification variables are
IF we consider only models that can be written like factorial models
(e.g., 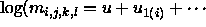 ) and include all
main effects, there are still 113 possible models. Even if all these
models had closed form estimates (which they don't) looking at all the
models would be difficult. As always, our prefer to have a
reasonable (fitting) model with a small number of parameters over a
similar model with more parameters.
) and include all
main effects, there are still 113 possible models. Even if all these
models had closed form estimates (which they don't) looking at all the
models would be difficult. As always, our prefer to have a
reasonable (fitting) model with a small number of parameters over a
similar model with more parameters.
Fienberg's book (1987) gives the following scenario for constructing a model for these data. (This ignores the graphical model stuff we have just been talking about. I will try to do a graphical model in a moment.)
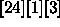
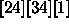
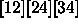
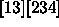 , and
, and 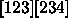
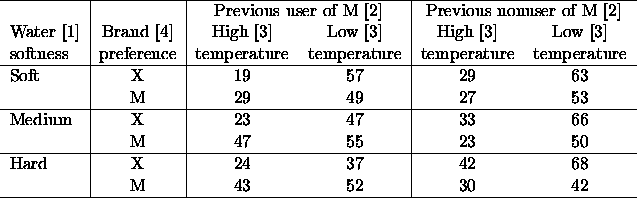
Lets start by getting in the data, and looking at it.
402 > ries <- fac.design(c(2,2,2,3),list(Temp=c("H","L"),
+ Pre=c("M","X"),Brand=c("X","M"), Soft=c("Soft","Med","Hard")))
402 > ries$Resp <- scan("ries-smith.dat")
402 > ries
Temp Pre Brand Soft Resp
1 H M X Soft 19
2 L M X Soft 57
3 H X X Soft 29
4 L X X Soft 63
5 H M M Soft 29
6 L M M Soft 49
7 H X M Soft 27
8 L X M Soft 53
9 H M X Med 23
10 L M X Med 47
11 H X X Med 33
12 L X X Med 66
13 H M M Med 47
14 L M M Med 55
15 H X M Med 23
16 L X M Med 50
17 H M X Hard 24
18 L M X Hard 37
19 H X X Hard 42
20 L X X Hard 68
21 H M M Hard 43
22 L M M Hard 52
23 H X M Hard 30
24 L X M Hard 42
Start by fitting the simplest model in the list above,
402 > glm(Resp ~ Temp+Pre+Brand+Soft, family=poisson, data=ries)
Call:
glm(formula = Resp ~ Temp + Pre + Brand + Soft, family = poisson, data = ries)
Coefficients:
(Intercept) Temp Pre Brand Soft1 Soft2
3.699209 0.2745538 0.0436785 -0.00793668 0.02687216 0.003092153
Degrees of Freedom: 24 Total; 18 Residual
Residual Deviance: 42.92866
Here is a list of the other models suggested above
[24][1][3]
glm(formula = Resp ~ Temp + Brand * Pre + Soft, family = poisson,
data= ries)
Degrees of Freedom: 24 Total; 17 Residual
Residual Deviance: 22.34719
[24][34][1]
glm(formula = Resp ~ Soft + Pre * Brand + Temp * Brand, family = poisson,
data = ries)
Degrees of Freedom: 24 Total; 16 Residual
Residual Deviance: 17.98559
[13][24][34]
glm(formula = Resp ~ Soft * Temp + Pre * Brand + Temp * Brand, family
= poisson, data = ries)
Degrees of Freedom: 24 Total; 14 Residual
Residual Deviance: 11.88649
[13][234]
glm(formula = Resp ~ Soft * Temp + Pre * Brand * Temp, family = poisson,
data = ries)
Degrees of Freedom: 24 Total; 12 Residual
Residual Deviance: 8.406872
[123][234]
glm(formula = Resp ~ Pre * Soft * Temp + Pre * Brand * Temp,
family = poisson, data = ries)
Degrees of Freedom: 24 Total; 8 Residual
Residual Deviance: 5.656044
In this case, note that the models are all nested: [123][234] > [13][234] > [13][24][34] > [1][24][34] > [1][24][3]. What was the good model?
In many respects this type of ``guided'' model selection is very satisfying. But, as with regression a more formal stepwise procedure is often helpful. Splus provides all the usual tools, so lets just let it go.
402 > step(mymod,scope=list(upper=~.^4,lower=~.^1))
Start: AIC= 54.9287
Resp ~ Pre + Soft + Temp + Brand
Single term additions
Model:
Resp ~ Pre + Soft + Temp + Brand
scale: 1
Df Sum of Sq RSS Cp
<none> 43.87621 55.87621
Pre:Soft 2 1.07484 42.80136 58.80136
Pre:Temp 1 1.25286 42.62335 56.62335
Pre:Brand 1 20.50510 23.37111 37.37111
Soft:Temp 2 6.07932 37.79688 53.79688
Soft:Brand 2 0.39516 43.48104 59.48104
Temp:Brand 1 4.35622 39.51998 53.51998
Step: AIC= 36.3472
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand
Single term deletions
Model:
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand
scale: 1
Df Sum of Sq RSS Cp
<none> 23.12993 37.12993
Pre:Brand 1 20.37267 43.50260 55.50260
Single term additions
Model:
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand
scale: 1
Df Sum of Sq RSS Cp
<none> 23.12993 37.12993
Pre:Soft 2 1.075196 22.05473 40.05473
Pre:Temp 1 1.253319 21.87661 37.87661
Soft:Temp 2 6.081331 17.04860 35.04860
Soft:Brand 2 0.395230 22.73470 40.73470
Temp:Brand 1 4.357797 18.77213 34.77213
Step: AIC= 33.9856
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand + Temp:Brand
Single term deletions
Model:
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand + Temp:Brand
scale: 1
Df Sum of Sq RSS Cp
<none> 18.33277 34.33277
Pre:Brand 1 20.37196 38.70473 52.70473
Temp:Brand 1 4.35039 22.68316 36.68316
Single term additions
Model:
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand + Temp:Brand
scale: 1
Df Sum of Sq RSS Cp
<none> 18.33277 34.33277
Pre:Soft 2 1.075230 17.25754 37.25754
Pre:Temp 1 0.691974 17.64079 35.64079
Soft:Temp 2 6.081616 12.25115 32.25115
Soft:Brand 2 0.395246 17.93752 37.93752
Step: AIC= 31.8865
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand + Temp:Brand + Soft:Temp
Single term deletions
Model:
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand + Temp:Brand + Soft:Temp
scale: 1
Df Sum of Sq RSS Cp
<none> 11.91664 31.91664
Pre:Brand 1 20.37144 32.28808 50.28808
Temp:Brand 1 4.35029 16.26693 34.26693
Soft:Temp 2 6.05905 17.97569 33.97569
Single term additions
Model:
Resp ~ Pre + Soft + Temp + Brand + Pre:Brand + Temp:Brand + Soft:Temp
scale: 1
Df Sum of Sq RSS Cp
<none> 11.91664 31.91664
Pre:Soft 2 1.088615 10.82802 34.82802
Pre:Temp 1 0.691996 11.22464 33.22464
Soft:Brand 2 0.343602 11.57304 35.57304
Call:
glm(formula = Resp ~ Pre + Soft + Temp + Brand + Pre:Brand + Temp:Brand + Soft:
Temp, family = poisson, data = ries)
Coefficients:
(Intercept) Pre Soft1 Soft2 Temp Brand Pre:Brand
3.682699 0.04343019 0.04342718 0.01564269 0.2782644 0.01658998 -0.1437655
Temp:Brand Soft1Temp Soft2Temp
-0.06836051 -0.05251834 -0.04906982
Degrees of Freedom: 24 Total; 14 Residual
Residual Deviance: 11.88649
We end up with a model that is at least familiar looking.
We could also proceed by looking at parameter values, again as we did in regression, but it is a little tricky.
402 > mymod <- glm(Resp ~ Soft*Pre*Temp*Brand, family=poisson, data=ries)
402 > summary(mymod)
Call: glm(formula = Resp ~ Soft * Pre * Temp * Brand, family = poisson, data = ries)
Coefficients:
Value Std. Error t value
(Intercept) 3.674892823 0.03362662 109.28523105
Soft1 0.034602276 0.04166801 0.83042779
Soft2 0.012394833 0.02349486 0.52755510
Pre 0.042297443 0.03362662 1.25785595
Temp 0.285673485 0.03362662 8.49545670
Brand 0.015236657 0.03362662 0.45311295
Soft1Pre -0.039962253 0.04166801 -0.95906306
Soft2Pre 0.016015575 0.02349486 0.68166297
Soft1Temp -0.045744735 0.04166801 -1.09783816
Soft2Temp -0.052760617 0.02349486 -2.24562393
Pre:Temp 0.025849868 0.03362662 0.76873229
Soft1Brand 0.012866861 0.04166801 0.30879469
Soft2Brand -0.001045718 0.02349486 -0.04450837
Pre:Brand -0.157008089 0.03362662 -4.66916072
Temp:Brand -0.064072675 0.03362662 -1.90541531
Soft1PreTemp 0.048167488 0.04166801 1.15598236
Soft2PreTemp -0.000712269 0.02349486 -0.03031595
Soft1PreBrand -0.062159775 0.04166801 -1.49178638
Soft2PreBrand -0.030357357 0.02349486 -1.29208509
Soft1TempBrand 0.012586592 0.04166801 0.30206845
Soft2TempBrand 0.007774692 0.02349486 0.33091034
Pre:Temp:Brand 0.050458667 0.03362662 1.50055726
Soft1PreTempBrand 0.010509090 0.04166801 0.25221001
Soft2PreTempBrand -0.019138419 0.02349486 -0.81457903
(Dispersion Parameter for Poisson family taken to be 1 )
Null Deviance: 118.6269 on 23 degrees of freedom
Residual Deviance: 0 on 0 degrees of freedom
Quite clearly the 4 factor interaction, and all the three factor
interactions can be removed, because of small t-values, which leaves
us with all the 2-factor interactions.
402 > mymod <- glm(Resp ~ (Soft+Pre+Temp+Brand)^2, family=poisson, data=ries)
402 > summary(mymod)
Call: glm(formula = Resp ~ (Soft + Pre + Temp + Brand)^2, family = poisson, data =
ries)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.107065 -0.4930669 0.02855437 0.5093409 1.386992
Coefficients:
Value Std. Error t value
(Intercept) 3.682222962 0.03328281 110.6343930
Soft1 0.043536098 0.04083575 1.0661272
Soft2 0.015051992 0.02294280 0.6560661
Pre 0.036165800 0.03309738 1.0927087
Temp 0.277223691 0.03296423 8.4098346
Brand 0.015077502 0.03315577 0.4547474
Soft1Pre -0.023416451 0.03912050 -0.5985724
Soft2Pre 0.017893207 0.02258248 0.7923490
Soft1Temp -0.050438215 0.04091668 -1.2327056
Soft2Temp -0.049901584 0.02296955 -2.1725101
Soft1Brand 0.017642716 0.03916083 0.4505195
Soft2Brand -0.002361722 0.02257536 -0.1046150
Pre:Temp 0.028578975 0.03322482 0.8601695
Pre:Brand -0.141752874 0.03193614 -4.4386345
Temp:Brand -0.064157285 0.03321404 -1.9316312
(Dispersion Parameter for Poisson family taken to be 1 )
Null Deviance: 118.6269 on 23 degrees of freedom
Residual Deviance: 9.846211 on 9 degrees of freedom
Now things get a little more interesting. It looks like we can get rid of Pre:Temp and Soft:Brand, but what else?
402 > summary(mymod <- update(mymod, . ~ . - Pre:Temp - Soft:Brand))
Call: glm(formula = Resp ~ Soft + Pre + Temp + Brand + Soft:Pre + Soft:Temp + Pre:
Brand + Temp:Brand, family = poisson, data = ries)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.207259 -0.395826 -0.02912609 0.4428775 1.363834
Coefficients:
Value Std. Error t value
(Intercept) 3.68213446 0.03329713 110.5841383
Soft1 0.04409441 0.04083153 1.0799107
Soft2 0.01492096 0.02294642 0.6502525
Pre 0.04385639 0.03187799 1.3757577
Temp 0.27826378 0.03293986 8.4476310
Brand 0.01662144 0.03311757 0.5018918
Soft1Pre -0.02717637 0.03867930 -0.7026076
Soft2Pre 0.01692800 0.02229341 0.7593277
Soft1Temp -0.05225327 0.04080825 -1.2804584
Soft2Temp -0.04923468 0.02290183 -2.1498144
Pre:Brand -0.14381446 0.03185316 -4.5149199
Temp:Brand -0.06847041 0.03277791 -2.0889194
(Dispersion Parameter for Poisson family taken to be 1 )
Null Deviance: 118.6269 on 23 degrees of freedom
Residual Deviance: 10.79797 on 12 degrees of freedom
The only likely suspect is Soft:Pre, so remove it.
402 > summary(mymod <- update(mymod, . ~ . - Pre:Soft))
Call: glm(formula = Resp ~ Soft + Pre + Temp + Brand + Soft:Temp + Pre:Brand
+ Temp:Brand, family = poisson, data = ries)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.433821 -0.3559708 -0.07358303 0.3974668 1.513481
Coefficients:
Value Std. Error t value
(Intercept) 3.68269868 0.03327911 110.6609783
Soft1 0.04342718 0.04080584 1.0642393
Soft2 0.01564269 0.02290053 0.6830710
Pre 0.04343019 0.03185253 1.3634772
Temp 0.27826441 0.03293940 8.4477687
Brand 0.01658998 0.03311667 0.5009554
Soft1Temp -0.05251834 0.04080584 -1.2870299
Soft2Temp -0.04906982 0.02290053 -2.1427374
Pre:Brand -0.14376554 0.03185253 -4.5134735
Temp:Brand -0.06836051 0.03277528 -2.0857337
(Dispersion Parameter for Poisson family taken to be 1 )
Null Deviance: 118.6269 on 23 degrees of freedom
Residual Deviance: 11.88649 on 14 degrees of freedom
Not much obvious left to do. This is the same model as before.
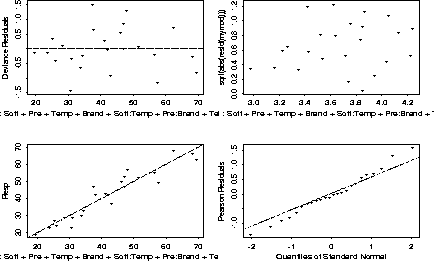
What is this model, and what does it mean? What are the diagnostics?
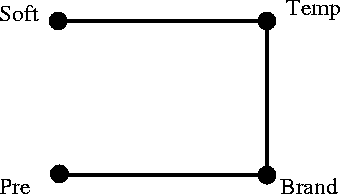
The model is quite easy to read. Soft and Pre and independent of each other, given Temp and Brand. Soft is independent of Brand given Temp, and Pre is independent of Temp given Brand.
Given the time-order of the variables, and what we know about water softness and washing temperature, we might be inclined to suggest possible cause-effect relationships by adding an arrowhead into Temp from Soft, and adding arrowheads from Pre and Temp into Brand.
A plot of the residuals also looks pretty good.
402 > motif() 402 > par(mfrow=c(2,2)) 402 > plot(mymod)