
Look at the stroke data. This is explicitly 0--1 data, and it is very hard to think about plotting it. A simple plot of, say, Status against WAB1, looks like the following, and it not all that informative.
402 > plot(WAB1, Status)

Even if I jitter the points a little, it is still not very easy to see any trends or patterns.
402 > plot(WAB1, Status+0.1*runif(length(Status)))
A somewhat more useful approach is to plot the data and add some sort of smooth curve that will allow you to at least look at some of the trends in the data. The particular approach I took with these data was to superimpose a (black-box) smooth curve generated by loess. The various pictures result from different smoothing parameters.
402 > scatter.smooth(WAB1, Status,span=0.2)
402 > title("Span = 0.2")
402 > scatter.smooth(WAB1, Status,span=0.35)
402 > title("Span = 0.35")
402 > scatter.smooth(WAB1, Status,span=0.5)
402 > title("Span = 0.5")
402 > scatter.smooth(WAB1, Status,span=0.65)
402 > title("Span = 0.65")
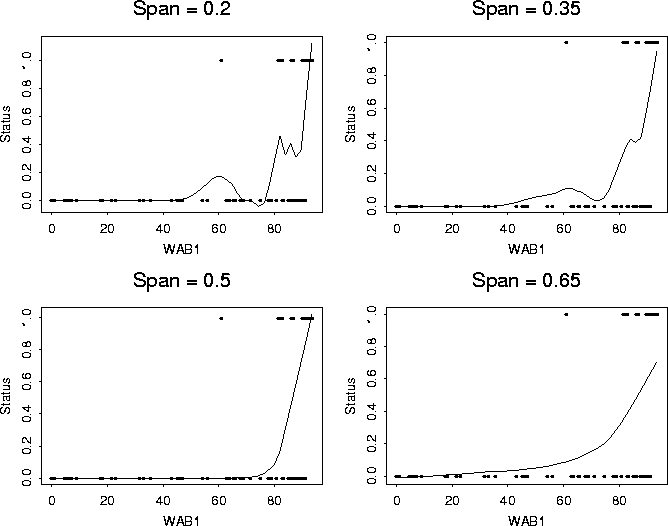
This is still not perfect, but you certainly get the sense that the probability goes up, probably more or less monotonely with WAB1.
Compare this to the similar picture(s) for Age.
402 > for (i in c(0.2, 0.35, .5, 0.65)){
+ scatter.smooth(Age, Status, span=i)
+ title(paste("Span = ", i))
+ }

If anything, there is a bit of evidence for some type of quadratic effect of Age, but the probable story is that Age is not that important, on its own. We should always remember that variables that do not seem to be important (from these marginal plots), may be quite important when paired with other variables (that is viewed conditionally).
With that hint about the Age variable, I re-ran the logistic regression model for these data and obtained,
402 > mymod <- glm(Status ~ Side + Gender + LOSD +WAB1 + Age + Age^2, family=bin>
402 > summary(mymod)
Call: glm(formula = Status ~ Side + Gender + LOSD + WAB1 + Age + Age^2, family =
binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.317304 -0.2637303 -0.0002506098 -6.014239e-07 2.770847
Coefficients:
Value Std. Error t value
(Intercept) -42.13652444 17.240544854 -2.444037
Side -1.70612965 1.320176507 -1.292350
Gender 4.03384776 1.847166535 2.183803
LOSD -0.28388626 0.130491084 -2.175522
WAB1 0.24891576 0.104667163 2.378165
Age 0.92453559 0.421765743 2.192059
I(Age^2) -0.00791642 0.003578441 -2.212254
(Dispersion Parameter for Binomial family taken to be 1 )
Null Deviance: 65.71913 on 60 degrees of freedom
Residual Deviance: 21.7621 on 54 degrees of freedom
402 > anova(mymod)
Analysis of Deviance Table
Binomial model
Response: Status
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 60 65.71913
Side 1 0.10011 59 65.61902
Gender 1 3.36010 58 62.25892
LOSD 1 13.46451 57 48.79441
WAB1 1 19.75552 56 29.03889
Age 1 0.05110 55 28.98780
I(Age^2) 1 7.22570 54 21.76210
This is somewhat surprising (because I didn't think there was an Age effect). Could we have seen the same trend from a residual analysis of these data?
Let us go back to the original model and look at residuals.

There is at least one large (Pearson) residual, and it is the same point as the large (deviance) residual. What about a plot of (deviance) residual against Age (when Age is in the model).
402 > mymod <- glm(Status ~ Side + Gender + LOSD +WAB1 + Age, family=binomial) 402 > scatter.smooth(Age, (residuals(mymod))) 402 > identify(Age, (residuals(mymod))) [1] 59 402 > scatter.smooth(Age[-59], (residuals(mymod))[-59])
We see that observation 59 is the one with the large residual. If I plot the data (the lower plot) without that observation, the quadratic trend seems to go away, at least a bit.

Observation 59 is now suspect, so let us remove that observation, and see what the resulting model looks like.
402 > WW <- rep(1, length(Side))
402 > WW[59] <- 0
402 > mymod <- glm(Status ~ Side + Gender + LOSD +WAB1 + Age,
+ weight=WW, family=binomial)
Warning messages:
linear convergence not obtained in 10 iterations. in: glm.fitter(x = X, y =
Y, w = w, start = start, offset = offset, family = family, ....
Oh-oh, what does that mean? (Basically, the optimization algorithm is converging slowly, which is an indication that there are some fitted probabilities that are very close to 0 or 1). We can try a few more iterations, via.
402 > mymod <- glm(Status ~ Side + Gender + LOSD +WAB1 + Age, + weight=WW, maxit=30,family=binomial)
Now, what does the summary and anova look like?
402 > summary(mymod)
Call: glm(formula = Status ~ Side + Gender + LOSD + WAB1 + Age, family = binomial,
weights = WW, maxit = 30)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.21685 -0.006138687 -2.107342e-08 -2.107342e-08 2.120409
Coefficients:
Value Std. Error t value
(Intercept) -46.034665461 23.60416082 -1.95027757
Side -7.479606389 4.79366143 -1.56031178
Gender 7.889726328 4.28891089 1.83956406
LOSD -0.677382165 0.43418335 -1.56012928
WAB1 0.662724777 0.34770876 1.90597667
Age -0.001289562 0.04096666 -0.03147832
(Dispersion Parameter for Binomial family taken to be 1 )
Null Deviance: 62.71879 on 60 degrees of freedom
Residual Deviance: 13.32727 on 54 degrees of freedom
Number of Fisher Scoring Iterations: 10
Correlation of Coefficients:
(Intercept) Side Gender LOSD WAB1
Side 0.8469550
Gender -0.9187997 -0.8860396
LOSD 0.7944690 0.9174434 -0.8555061
WAB1 -0.9831416 -0.9061715 0.9317554 -0.8758313
Age -0.0387868 0.0615410 0.0243350 -0.0022418 -0.0596445
Warning messages:
1 rows with zero weights not counted in: summary(mymod)
If I now start adding the quadratic term in Age, I get myself into all sorts of trouble.
402 > formula(mymod)
Status ~ Side + Gender + LOSD + WAB1 + Age + Age^2
402 > anova(mymod)
Analysis of Deviance Table
Binomial model
Response: Status
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 60 62.71879
Side 2 0.62858 58 62.09021
Gender 1 2.34693 57 59.74328
LOSD 1 13.67051 56 46.07277
WAB1 1 32.74451 55 13.32826
Age 1 0.00099 54 13.32727
I(Age^2) 1 13.32727 53 0.00000
Warning messages:
1: linear convergence not obtained in 10 iterations. in: glm.fit(x, y, w,
offset = offset, family = family, maxit = control$maxit, ....
2: linear convergence not obtained in 10 iterations. in: glm.fit(x, y, w,
offset = offset, family = family, maxit = control$maxit, ....
Whoa. What is going on here? We suddenly have a model that fits perfectly?
The summary looks even weirder?
402 > summary(mymod)
Call: glm(formula = Status ~ Side + Gender + LOSD + WAB1 + Age + Age^2, family =
binomial, weights = WW, maxit = 50)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.9065e-05 -2.107342e-08 -2.107342e-08 -2.107342e-08 3.281089e-05
Coefficients:
Value Std. Error t value
(Intercept) -2858.6085408 2227320.001 -0.0012834297
Side -164.0618144 165491.082 -0.0009913635
Gender 273.5752941 237195.052 0.0011533769
LOSD -16.2464405 13633.473 -0.0011916582
WAB1 24.1122280 17153.825 0.0014056473
Age 39.8782980 35880.527 0.0011114190
I(Age^2) -0.3549147 302.566 -0.0011730157
(Dispersion Parameter for Binomial family taken to be 1 )
Null Deviance: 62.71879 on 60 degrees of freedom
Residual Deviance: 0 on 53 degrees of freedom
Number of Fisher Scoring Iterations: 29
Correlation of Coefficients:
(Intercept) Side Gender LOSD WAB1 Age
Side 0.3661039
Gender -0.8397332 -0.5132934
LOSD 0.7676113 0.5867586 -0.7405370
WAB1 -0.9678428 -0.5023038 0.8384746 -0.7822973
Age -0.9537356 -0.2802197 0.7986261 -0.8085521 0.8643352
I(Age^2) 0.9585630 0.3372172 -0.8129406 0.8428222 -0.8863173 -0.9963403
Warning messages:
1: fitted values close to 0 or 1 in: family$deviance(mu, y, w, residuals = T)
2: 1 rows with zero weights not counted in: summary(mymod)
402 >
On reflection, it is clear what is going on. Look at the first plot of Status against WAB1. Here we see, that absent the one observation in the middle (which is 59), we have an almost perfect discimination between the two levels of Status. That is the clue to what is ``broken''. With the 7 parameters (anything like WAB1 squared would have done), we can find a function that perfectly discriminates between the two levels of status, and then maximum likelihood modelling breaks down. There is a lot more to be said here, I just don't know what it is.