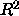The model

The S-Plus logistic regression command needs to know both the number of successes and the number of failures, so we need to start out by creating such a variable,

402 > FN <- cbind(Fail, n-Fail)

Now, just use the glm command, with the family=binomial option, to fit the model, viz.

402 > mymod <- glm( FN ~ Temp, family=binomial)
402 > mymod <- glm( cbind(Fail, n-Fail) ~ Temp, family=binomial)

Either of the above forms will work, but the first is easier in the long run. Now look at the results of the fit,

402 > summary(mymod)

Call: glm(formula = FN ~ Temp, family = binomial)
Deviance Residuals:
        Min         1Q     Median          3Q      Max 
 -0.9522773 -0.7829968 -0.5411832 -0.04378972 2.651492

Coefficients:
                 Value Std. Error   t value 
(Intercept)  5.0848620  3.0477855  1.668379
       Temp -0.1155992  0.0469317 -2.463136

(Dispersion Parameter for Binomial family taken to be 1 )

    Null Deviance: 24.23036 on 22 degrees of freedom

Residual Deviance: 18.08633 on 21 degrees of freedom

Number of Fisher Scoring Iterations: 4 

Correlation of Coefficients:
     (Intercept) 
Temp -0.9932182 
402 > anova(mymod)
Analysis of Deviance Table

Binomial model

Response: FN

Terms added sequentially (first to last)
     Df Deviance Resid. Df Resid. Dev 
NULL                    22   24.23036
Temp  1 6.144035        21   18.08633

The model fits well (although, just like 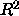is regression, one should be cautious about this), and the temperature coefficient is certainly significant.

At this point we need to

• Get predictions for the low-temperature extrapolations, and
• Evaluate the fit of the model

• Extrapolating
• Evaluating the Model