Extrapolating

Lets work on that, in that order (which is really back-to-front, but useful for teaching purposes).

The fitted values (on the probability scale) are obtained via,

402 > fitted(mymod)
         1         2         3          4          5          6          7 
 0.2607849 0.1817866 0.1652202 0.09994062 0.07278457 0.06535816 0.06535816
          8          9         10         11         12         13         14 
 0.06535816 0.05864156 0.05257638 0.04710711 0.04710711 0.04710711 0.04710711
         15         16         17         18         19         20        21 
 0.03775043 0.03376847 0.02698616 0.02698616 0.02411117 0.02411117 0.0192299
         22         23 
 0.01716665 0.01367159

The predicted values (on the logit scale) are,

402 > predict(mymod)
         1        2         3         4         5         6         7 
 -1.041893 -1.50429 -1.619889 -2.197885 -2.544682 -2.660281 -2.660281
         8        9        10        11        12        13        14 
 -2.660281 -2.77588 -2.891479 -3.007079 -3.007079 -3.007079 -3.007079
        15        16        17        18        19        20        21 
 -3.238277 -3.353876 -3.585074 -3.585074 -3.700673 -3.700673 -3.931872
        22        23 
 -4.047471 -4.278669
402 > fitted(mymod) - unlogit(predict(mymod))
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 
 0 0 0 0 0 0 0 0 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0

(unlogit is the following simple function),

402 > unlogit <- function(x) { exp(x)/(1 + exp(x)) }

For communication purposes, it makes sense to work on the probability scale (and hence use fitted), but for all other purposes the predicted values are what we want. In particular, the predict function has an option that will give the Standard Errors of the predicted values (on the logit scale), viz.,

402 > predict(mymod,se=T)
$fit:
         1        2         3         4         5         6         7 
 -1.041893 -1.50429 -1.619889 -2.197885 -2.544682 -2.660281 -2.660281
         8        9        10        11        12        13        14 
 -2.660281 -2.77588 -2.891479 -3.007079 -3.007079 -3.007079 -3.007079
        15        16        17        18        19        20        21 
 -3.238277 -3.353876 -3.585074 -3.585074 -3.700673 -3.700673 -3.931872
        22        23 
 -4.047471 -4.278669

$se.fit:
         1         2        3         4         5         6         7 
 0.7682786 0.5943294 0.556385 0.4298909 0.4298809 0.4441498 0.4441498
         8         9        10        11        12        13        14 
 0.4441498 0.4647341 0.4908397 0.5216385 0.5216385 0.5216385 0.5216385
        15        16        17        18        19        20        21 
 0.5942932 0.6348851 0.7222049 0.7222049 0.7682357 0.7682357 0.8637766
        22       23 
 0.9129226 1.013299

$residual.scale:
[1] 1.189907

$df:
[1] 21

So, a 95% confidence interval for the first predicted value on the logit scale would be

Transferred to the probability scale, this is an interval , with a center at .

But what about predictions nearer the take-off temperature?

 predict(mymod, data.frame(Temp=c(30,31,32,33)), se=T)
$fit:
        1        2        3       4 
 1.616887 1.501288 1.385689 1.27009

$se.fit:
        1        2        3       4 
 1.972255 1.917739 1.863302 1.80895

(That was pretty sneaky, but the predict function requires a data frame predictor values).

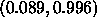The bottom line is that at F our model extrapolates to , with a 95% confidence interval of , which is VERY wide. Even with this wide interval, the point estimate is something to worry about.