Contrasts

It is useful to get standard errors with the estimates of the coefficients of the ANOVA model. For the cell means model this is easy. The model says

and hence

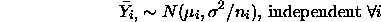
The independence makes it easy to compare pairs of cell means also:

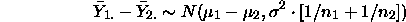
and similarly with interesting linear combinations:

When we replace 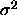with the usual regression estimator MSE, of course, all the 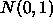's get replaced by 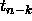's.

In the blood coagulation data it is interesting to think about whether 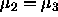, and perhaps whether 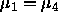. 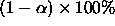confidence intervals for the differences in cell means are:

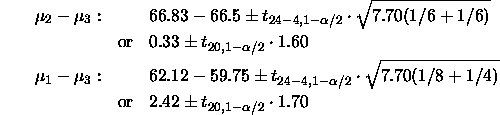
Both intervals contain zero; inverting these intervals to make hypothesis tests we would not have any evidence to reject the null hypotheses of equality.

There are two things to note about this example: one is nomenclature and the other is a warning.

• Contrasts: The parameters (and their estimates) are called contrasts: they contrast the values of two different cell means.

  As ANOVA and linear models developed, the meaning of the word contrast has also expanded: nowadays, a contrast is any linear combination of the cell means 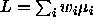where the coefficients sum to zero, .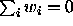

  Equation (1) lets us estimate and test hypotheses about any contrast L.

  Sets of contrasts are sometimes used to reparameterize an ANOVA model to make it easier to work with numerically (that is the point of the ``Helmert contrasts'' that you may have read about in the SPLUS Guide to Statistics). In cases like this, the parameters or ``effects'' of the reparametrized model are also contrasts. This is confusing, but that's the way the nomenclature works.

• The analysis we illustrated with the contrasts and was flawed in two ways:
  1. Capitalizing on chance: We looked at the data (sample cell means) to decide which contrasts to consider. This is bad news, since the distribution theory that leads to the and distributions above depend on not having looked at the data yet for their validity. (Nevertheless this is a common exploratory device. Any results obtained this way would need to be confirmed in an independent replication of the experiment, however.)

  2. Multiple Comparisons: We didn't make any adjustment for the fact that we calculated two confidence intervals (or performed two hypothesis tests) instead of one. This is the multiple inference or multiple comparisons problem. Just because each interval individually has confidence 95% (say), it does not mean that both intervals together have this confidence: Indeed, letting

     

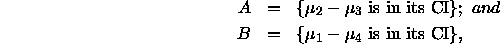
     we see from

     

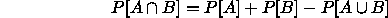
     that it would be quite unusual if A, B and all had probability 0.95 (say).