Comments

April 15:

1. I am not an expert on any of this! I created the page out of frustration that I could not find any such brief set of suggested resources. I'm not sure how well I'll do at updating it. It would be GREAT if someone else did a better job, and updated it! I would, however, very much appreciate comments and suggestions.
2. I am trying to stick mainly to science and avoid policy. Of course, we care about the science in large part for its value in making policy, and there are places where it is interesting to see how the scientific knowledge will be used. An example is the April 17 guide for governors by an expert committee at Johns Hopkins. There is a lot that could be done to better understand and improve the human process of making decisions in the presence of uncertainty.
3. If you look at the modeling results in the published papers, you will be struck by the very large uncertainty throughout. It is crucial to keep in mind the large uncertainties in the projections---they are not necessarily "wrong" in what they predict if their estimates are off, even by a fair amount, unless the estimates are off by so much as to deviate beyond what their estimated uncertainty would suggest to be fairly likely. I should add that the reported uncertainties are themselves based on the models and, thus, on the modeling assumptions. As always, even the most informative scientific conclusions should be taken as guides to understanding: a little illumination keeps us from stumbling in the dark, but it can not transport us to our destination. Concerning COVID projection uncertainty see the FiveThirtyEight survey results (below), and the NY Times article on the uncertainties (below).
4. Published papers from reputable journals vary in quality, and strength of evidence. Furthermore, a lot of the papers (including some in the links I am sharing) have either not yet been reviewed, or were given expedited review---which suggests it is appropriate to have an extra bit of scientific skepticism about aspects we can't judge for ourselves.
5. There are many, many scientific issues surrounding COVID-19 and some of the ones I omit from the web page have interested me enough to take a look. There are, of course, a lot of publications based on lab experiments (which I tend to like), though they are sometimes coupled with observational data. I will mention the number, and relative number, of ACE2 receptors in the lung and heart, in relation to ACE inhibitor blood pressure meds, which I happen to take. Turns out the evidence about ACE inhibitors is mixed (I'm inclined to believe the "protective" results rather than the "increased risk" results). A nice blog entry about the issue is here and a review is here.
6. Of particular interest is a key variable (which my physician-wife Loreta and I have talked about a lot): inoculum size. This almost never gets discussed, mainly, I presume, because it's nearly impossible to measure or estimate, except in a laboratory setting. There's a helpful lab study, on humans exposed to H1N1, here. For me, the main findings are (i) inoculum size matters to both probability of getting the disease and severity of symptoms and (ii) there is very large variation across subjects (people). See this figure. Also, there's nice New Yorker article that discusses this and related issues.
7. Concerning the projection methods themselves, there are two general approaches. One we might call purely predictive. A very popular website with predictions (projections) is produced by a health metrics organization in Seattle, affiliated at least loosely with the University of Washington, called IHME. Their projections are used by the White House Task Force. The methodology is relatively simple, and may be described as curve fitting. In the original version they assumed the death rate over time in each U.S. state would evolve similarly to the way it evolved in Wuhan. A link to their methodology is given below. Subsequent projections have used more recent data, from places other than China, to form baseline accumulated death curves. This change in baseline, however, can lead to noticeable changes in predictions. Furthermore, as I said, the method is simple (a bit more description is in the additional comments, below), and would seem perhaps too simple for many purposes. For example, the assumed similarity among death rate curves may have trouble accommodating the inhomogeneity across locations, especially as one starts to extrapolate more than a short period into the future. A list of cautions about the IHME model can be found here.
The second approach applies some version of a well-established epidemiological framework called SEIR modeling (often in a slightly simpler form called SIR). The acronym comes from the stages (we usually call them compartments) each patient must travel through: Susceptible, Exposed, Infected, Removed (i.e., removed from the susceptible population because they are either recovered or deceased). Here, in addition to deaths, one must consider infection rates, and the model can be complicated. Modern forms are statistical, meaning that particular features of the data are assumed to follow probability distributions; this also allows calculation of uncertainty. See additional comments, below. Predictions by the group at Imperial College have received a lot of attention and are favored by the British government; a link to their paper on predictions for many European countries, and a few non-European ones, is given below. They explicitly assume particular forms for several probability distributions based on data from China (and other experience in the literature), and they consider a more involved set of interventions, modeled as affecting the rate of transmission. Interestingly, IHME projections turned out to produce very much higher predicted deaths for the UK than projections using SEIR-style models. My own inclinations lean toward the more detailed modeling approach, and, from what I gather, I tend to think the chief groups doing the SEIR-style European and UK projections are likely to be somewhat more careful and trustworthy. Also, the first approach can be done differently, and made very much more sophisticated, as implemented by the Delphi group here at Carnegie Mellon. They have done extremely well in the past, winning many national competitions in flu forecasting. For Covid-19 they are relying on different kinds of inputs: human judgment from large numbers of humans (filling out short surveys online); human behavior, such as searches in Google (e.g., for products relevant to cold symptoms or for information about the disease); and some anonymized patient and patient-testing data (via certain providers and labs). As I understand things, they hope to improve immediate prevalence estimation and short-term predictions. Because the group is embedded in the wider disease forecasting community (including through the CDC, which requested their effort on this), their results could feed into others aimed at informing policy.

April 19

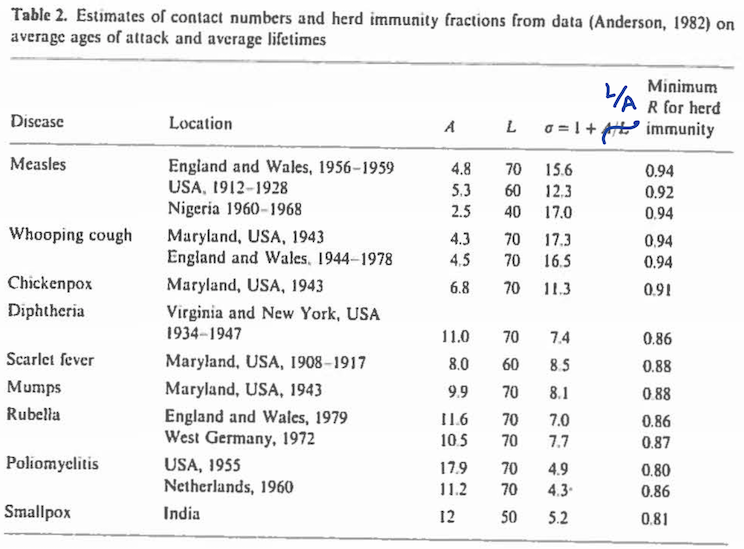
8. An extremely important topic is what's usually called "herd immunity." This refers to a stable situation in which every new outbreak will die out, rather than exploding to something unmanageable. From an epidemiological perspective, the main goal is to figure out what percentage of the population needs to become immune, through either exposure or vaccination, in order to reach herd immunity. Here, modeling has been very helpful. I give some links in additional comments, but let me say two things now.
First, the simplified theory (using the basic SIR differential equations) provides easily-computed formulas (links below). An informative table for multiple childhood diseases, based on work from the late 1970s and early 1980s (and taken from a 1989 overview found below) may be found here. In that table the lowest percentage immune needed for herd immunity occurs for polio, at 80%. That is, polio becomes manageable once at least 80% of the susceptible population is immune. Other, more highly communicable diseases require higher percentages, e.g., measles requires around 93%. These are, of course, data-based estimates and are subject to uncertainty. The lesson for Covid-19, however, seems clear: because Covid-19 is highly contagious, it would seem at first glance that very high levels of immunity may be required. On the other hand, a second point is that the population of susceptibles is inhomogeneous. The simplest case is if there are two distinct sub-populations, which, in the case of Covid-19, we might imagine to be, say, young and non-compliant (high spreading of the disease) and older, more compliant (lower spreading of the disease). In this case, assuming the young and old interact, but there's much less spreading from young to old than from young to young, the fastest spreading would occur within the young sub-population, and the most important thing to know would be the degree of immunity among the young. This becomes analogous to many childhood diseases. It should provide a more optimistic outlook insofar as immunity among the young could be expected to be much higher than among the old. The literature is full of discussion about situations involving inhomogeneous populations (e.g., see the papers below), but what I've just said is my own speculation. I don't know of good data and modeling to help with analysis of Covid-19 based sub-populations (which would also have to consider special outbreak situations, as in nursing homes), but I presume such data and analysis will come.

April 20

9. It is important, I think, to realize that the immediate goal of public health efforts is not eradication of the disease but, rather, control of it, where an explosive, widely-spread epidemic is avoided. In my additional comments, below, I mention that the proportion immune needed for herd immunity is based on the assumption that with herd immunity we move to an endemic stage, meaning that the epidemic is gone, but the disease remains in the background. Furthermore, apparently, for the diseases in the cited table immunity is permanent, whereas for the SARS coronaviruses it is likely to taper off across time. This suggests that the proportion immune will itself be dynamic. Also, another unknown is the rate at which this virus might mutate in disease-relevant ways. Endemic Covid-19 would become tolerable if there were treatments that often help patients substantially.

April 22

10. There many issues associated with vaccine development, as discussed here on March 30 and here on April 9. A technical overview of modern methods may be found here. There are statistical issues, too, and a nice-looking 2009 book by Halloran, Longini, and Struchiner, but I haven't yet found a recent overview.