Contributions to Analysis of Neural Spike Train Data

My papers on spike train analysis can be put in 5 categories, listed immediately below. The context and content of these papers are explained in subsequent sections:

Background: Spike Trains as Point Processes
Spike Counts and Trial-Averaged Firing Rate
Within-Trial Analysis
Multiple Neurons
Decoding and Brain-Machine Interface
The problems attacked have also been treated by other authors, but here I omit references to that other work. Analysis of local field potentials (LFPs) became a substantial component of our research; publications based on LFPs (or both spike trains and LFPs) are intermingled. This page was updated June 2024.

A 2018 overview of computational neuroscience may be found in this review article and a 2023 review of methods for identifying cross-population interactions may be found here.

Background: Spike Trains as Point Processes

NOTE: LFPs, which are low-pass filtered (smoothed) versions of the raw voltage recordings, are generally considered to represent the summed voltage contributions generated at synapses in the neighborhood of the electrode. There are disagreements about the spatial extent of this "neighborhood," see references in our 2023 review (linked above near the beginnng of this page). Spike trains instead result from high-pass filtering of the voltage recordings, followed by a process of assigning apparent action potentials to particular neurons (as more than one neural source is picked up by the electrode), which is known as "spike sorting."

One of the most important techniques in learning about the functioning of healthy and diseased brains has involved examining neural activity in laboratory animals under varying experimental conditions. Neural information is represented and communicated through series of action potentials, or spike trains (Kass, 2014). Numerous investigations have documented the way neural firing rate increases in response to a sensory stimulus, or preceding an action.

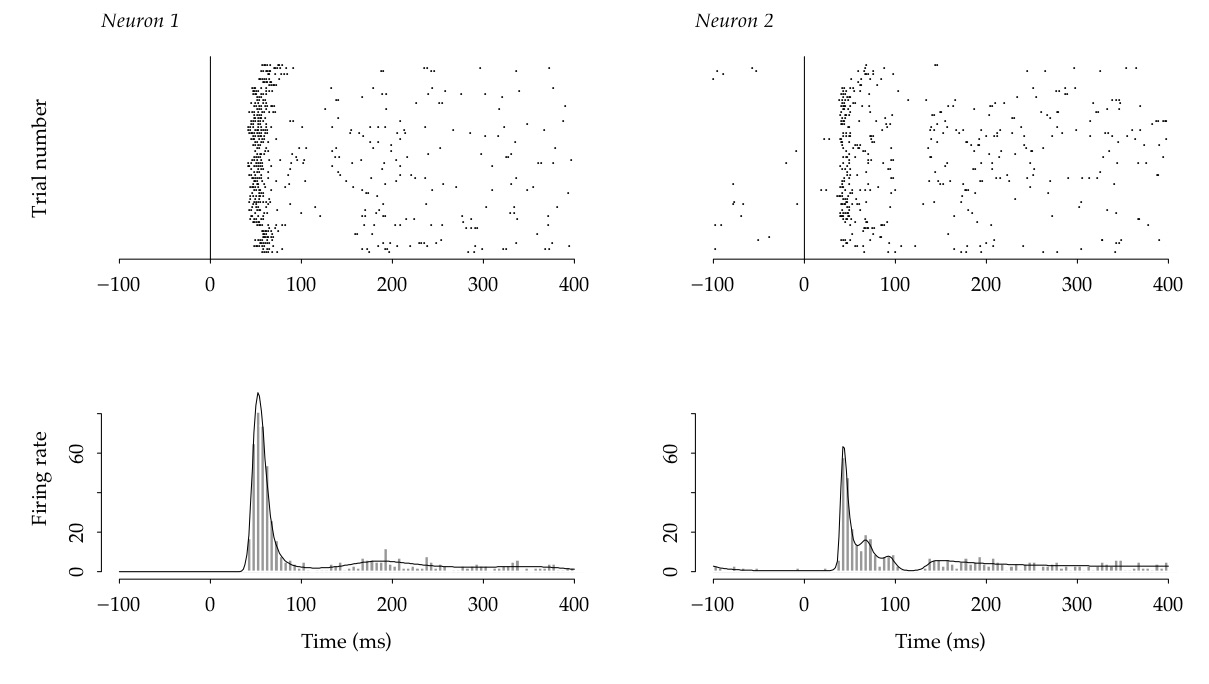
Figure 1: Raster plots (top) and Peri-Stimulus Time Histograms (PSTHs, bottom) from two neurons recorded simultaneously in primary visual cortex. Each line of a raster plot displays spike times, as dots, for one experimental trial. Spike times in each raster plot are aggregrated into 5 millisecond bins, then counted and displayed in the corresponding PSTH, in units of spikes per second. The solid curves are the smoothed estimates of trial-averaged firing rate , and were obtained using BARS (which will be explained below).

The top two panels of Figure 1 display spike trains recorded simultaneously from two neurons in primary visual cortex during 64 replications, or trials, of a single experimental condition. In each of the lower panels of Figure 1 the data have been aggregated across trials into bins of width delta t = 5, and normalized to units of spikes per second, yielding a Peri-Stimulus Time Histogram (PSTH). This pair of PSTH plots shows a clear change in firing rate across the several hundred milliseconds following time zero, which refers to the onset of a visual stimulus.

Based on a large sample of data, the firing rate (FR) across a substantial interval of time could be defined as FR=(number of spikes)/(interval of time). However, it is desirable to avoid dependence on a specific time interval; furthermore, as may be seen in Figure 1, spikes occur irregularly both within and across repeated trials. It is therefore reasonable to think of a spike train as a stochastic sequence of isolated points in time, i.e., as a point process, and to introduce a theoretical, instantaneous firing rate in the form of the point process intensity function. Analyses of trial-averaged firing rate involve trial-aggregrated data, where the trial identity of each spike time is ignored. In point process terminology, the trial-averaged firing rate is the marginal intensity function. The PSTH may be considered an estimate of the marginal intensity function. Analyses of within-trial firing rate, on the other hand, involve the original spike trains themselves, without aggregration, and are based on the conditional intensity function. Letting H_t denote the history of spike times prior to time t, the point process probability density function, and thus the likelihood function, may be written in terms of the conditional intensity function lambda(t | H_t), which is also the hazard function for the waiting time distribution (waiting for the next spike). On a given experimental trial the conditional intensity determines the conditional probability that the next spike will occur at time: P(spike in (t, t + dt)| H_t)= lambda(t | H_t)dt. In the Poisson case the process is memoryless and the conditional intensity reduces to the history-independent form lambda(t | H_t) = lambda(t).

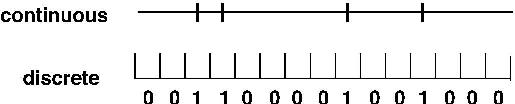
Figure 2: Spike trains are measured in discrete time but are conceptualized in continuous time. In each time bin a 1 indicates a spike has occurred. The sequence of 1s and 0s then form a binary time series.

Spike times are recorded to fixed accuracy delta t. An observed spike train is thus a binary time series, as pictured in Figure 2. It is not hard to show that the point process likelihood function approximates the corresponding binary time series likelihood function, for small delta t. Typically delta t = 1 millisecond and the approximation is very good. Importantly, this means that if a point process model sets log lambda(t | H_t) equal to some function of covariates, the spike train data may then be analyzed using generalized linear models and familiar variants of them.

From 1998 to 2010 All of the foregoing was discussed by Brillinger, notably in a 1988 paper in Biological Cybernetics, but no new insights into neural behavior were offered and the main ideas did not begin to penetrate the neurophysiology literature until at least 10 years later. In 1998 Emery Brown and colleagues published a paper that introduced state-space modeling, in the context of point processes, to neuroscience. That year he and I decided to learn about existing approaches to spike train data analysis with the goal of writing a review article. As Emery and I dug into the literature we discovered gaping holes, holes so large that we could not write a review until they were filled. With various colleagues Emery and I, mostly separately, worked on several problems, as did some other statistically-oriented researchers in neurophysiology. Finally, by 2005, together with Valerie Ventura, we were able to finish and publish the review article we had set out to write 7 years earlier (Kass, Ventura, Brown, 2005; see also Brown, Kass, and Mitra, 2004). Along the way, in 2002, Emery and I began a series of international workshops Statistical Analysis of Neural Data (SAND), bringing together experimenters, computational neuroscientists, and statisticians. It is impossible to say what impact these research and outreach efforts had on the field, but the quality of statistical analysis of spike train data improved dramatically over this period. The first SAND meeting devoted considerable time to problem definition. At the fifth SAND meeting, in 2010, investigators reported development and application of state-of-the-art statistical methodology in attacking well-formulated and important scientific questions. (See Brown and Kass, 2007; Kass, 2010a.) Our experiences during this time prompted reflections on the nature of statistics and statistical training (Brown and Kass, 2009), and on the connections between statistical practice and the foundations of statistical inference (Kass, 2010b, 2011).

Since 2010 Subsequent work has moved more systematically into analysis of simultaneously-recorded multiple spike trains. Challenges often involve regularization and, increasingly, inferences about cross-area coupling (e.g., Vinci et al., 2018b). A major review of computational neuroscience, with an emphasis on the complementarity of mathematical and statistical modeling of spike train data, was given by Kass and 24 others in 2018 in the Annual Reviews series and may be found here. Also, in 2014 Emery and I, together with Uri Eden, published our textbook Analysis of Neural Data.

Spike Counts and Trial-Averaged Firing Rate

The large majority of published findings have been based on trial-averaged firing rates, often using elementary comparisons (e.g., t-tests) of spike counts obtained over windows of time where a neuron appeared to be active. A comparatively sophisticated yet still simple example is in Suway et al. (2017). Early on, my Pittsburgh colleagues made me aware of two shortcomings in spike count comparisons: (1) they can not produce fine structure in trial-averaged rates, such as the time at which the maximal firing rate occurs, and (2) the window used in spike count analysis is arbitrary. We responded by adapting existing smoothing methods (Olson et al., 2000; Ventura et al., 2002) and developing powerful new smoothing methods (DiMatteo, Genovese, and Kass, 2001). The new methods were based on Bayesian Adaptive Regression Splines (BARS), which solves generalized nonparametric regression problems with regression splines by using reversible-jump MCMC to find good knot sets.

Our initial research showed that (i) after aggregating across trials the spike times may often be assumed to follow an inhomogeneous Poisson process, (ii) Poisson nonparametric regression splines could provide a useful methodology for answering scientific questions of the sort frequently found in neurophysiological investigations, and (iii) when fixed-knot regression splines (or more generally, fixed-bandwidth smoothers) were inadequate, BARS did an excellent job of estimating the marginal intensity function. Figure 1 illustrates such a situation, where a sudden increase in firing rate occurred. We documented the very good frequentist properties of BARS, both small mean squared error and accurate coverage probability of posterior intervals. We have yet to find any example where another nonparametric method can produce a smaller mean squared error. We provided a good implementation of BARS, especially in the Poisson case we cared most about--because it applies to marginal intensity functions--where we incorporated earlier stepwise knot selection code produced by Charles Kooperberg. The software was put into the CRAN library and was described in Wallstrom, Kass, and Liebner (2008). A Matlab version was also created by Ryan Kelly. Kass (2008) gives an overview for neuroscientists.

We then used BARS to (i) assess variability of marginal intensity functions across multiple neurons, (ii) test equality of two or more marginal intensity functions, and (iii) estimate directional tuning functions. Results from (i), reported in Behseta et al. (2005), showed that the proportion of variation explained by the first principal component based on näive functional data analysis (FDA) can be severely biased upwards because it ignores the variability in estimation of the functions. In a simulation study based on our earlier analysis of 347 neurons from primary motor cortex, the method was 8 times more accurate than näive FDA. Our results from (ii), in Behseta and Kass (2005) and Behseta et al. (2007), provided what we considered to be an elegant answer to the question, ``Which time window should I use to compare firing rates?'' In our methods we used the entire experimental time interval to compare the marginal intensity functions: we chose a grid of time points at which to evaluate the two BARS estimates, retained the BARS covariance matrices, and applied a modified MANOVA. The modifications dealt with covariance matrices that were known but unequal and singular, and in Behseta et al. (2007) we derived the appropriate likelihood ratio tests (building on results that had appeared in the statistics literature about 10 years earlier). The methods are general and, in fact, we have also applied them to a problem in MEG imaging (Wang et al., 2010, Journal of Neurophysiology). For (iii) Kaufman, Ventura, and Kass (2005) developed an extension of BARS for circular applications, called cBARS, using a periodic spline basis. We showed that cBARS can provide the same kind of improvements compared to circular smoothing splines that BARS provides in the usual settings.

Within-Trial Analysis

Numerous papers in the literature have relied on the Poisson assumption, even though it has been known for a long time that spike trains are often discernably non-Poisson both in theory, according to stochastic differential equation models, and in practice. In parallel with our work on marginal intensities, for trial-averaged firing rates, we have developed methodology based on conditional intensity functions for non-Poisson within-trial analysis. This has several components. First, it is important to know how sensitive methods are to realistic departures from Poisson processes. Second, it is very helpful to have models that can accommodate non-Poisson point processes, where spiking history comes into play. Third, it is sometimes possible and desirable to characterize trial-specific effects, including sources of trial-to-trial variability. This requires within-trial methodology.

In general lambda(t | H_t) could be a complicated function of the entire spiking history. Some assumption must be introduced to reduce the effective dimensionality of the problem. One approach, applied by Brown and colleagues in a 2001 paper, is to modulate the firing rate of a renewal process by rescaling time. The resulting models require special-purpose nonlinear fitting. Kass and Ventura (2001) observed that models could be fitted with standard generalized linear models software when the dependence of firing rate on the time intervals between past spikes (spikes before time t) is described by splines. The GLM-based approach of Kass and Ventura (2001), including its many generalizations, has become standard. Because models of this type are based on a generalized regression framework, a descriptive term for them is point process regression models. Koyama and Kass (2008) provided a detailed comparison of the Brown et al. and Kass and Ventura approaches using simulated spike trains based on integrate-and-fire models, which are fundamental to theoretical neuroscience. The main results were that each of the two statistical models could fit slightly better than the other in particular situations--depending on the source of variability in the neural input current--but both generally fit this theoretical model far better than the inhomogeneous Poisson process. The approach of Kass and Ventura differed in one detail from the version used by Pillow and colleagues in a well-known 2008 paper in Nature . Chen et al. (2019) showed that the form used by Kass and Ventura is less likely to suffer from a kind of instability that had been noted by Truccolo and colleagues in a 2017 paper. In Wang et al. (2015) we noted that in some slice experiments (ex vivo) standard log-additive non-Poisson models tend to under-fit the peak firing rate as a function of stimulus, and we showed that an ad hoc fix can perform better (an elegant solution to this difficulty remains an outstanding problem as of 2016).

In addition to investigating non-Poisson models of spike train irregularity we have developed complementary methods of handling two other aspects of variability that are important for within-trial analyses. After Ventura (2004, Neural Computation ) had provided a simple approach to characterizing onset latency (roughly speaking, the time at which increased firing occurs), Ventura, Cai, and Kass (2005b) showed how trial-to-trial gain modulation (amplitude variation in firing rate) could be accommodated in the generalized linear modeling framework by using low-dimensional splines to represent deviations from the trial-averaged rate. At the urging of several collaborators we also attacked the problem of burst detection. In many contexts a neuron will suddenly, and erratically, ``turn on'' and fire a rapid succession of spikes after which it will return to its resting firing rate. Bursting behavior has been studied theoretically using differential equations, but empirically bursts do not always occur as easily-identified clusters of successive spikes and a small literature has been devoted to automatic burst detection. One initial thought might be to use a hidden Markov model to represent the unknown binary burst/non-burst state, but bursting tends to be more irregular than exponential waiting times allow. In Tokdar et al. (2009) we developed a hidden semi-Markov model (generalizing the waiting-time distribution) and a fast Gibbs sampling algorithm for fitting, and we showed that this new method could out-perform existing approaches. A different, but related problem is identify oscillatory behavior in spike trains. In many contexts oscillations may be expected, but because of the erratic nature of neural spiking they can be hard to assess statistically. In Arai and Kass (2017) we develop methodology based on constrained auto-regressive latent processes to pull out the oscillation, if it exists.

During an extended visit to the University of California, Berkeley, I began a collaboration with Vincent Vu, who was then a student working with Bin Yu. A tool favored by many physics-oriented theoretical neuroscientists is mutual information, but most data-based calculations have used naive methods for estimation of information. In Vu et al. (2007) we showed how a method developed in ecology to estimate diversity in the presence of unseen species could be used for neural applications; we proved consistency and optimality of the approach; and we showed that it could behave better than existing alternatives in finite samples. A conceptual difficulty in using mutual information is its reliance on stationarity: in many cases the stimulus itself is already non-stationary, making the definition of mutual information void. In Vu et al (2009a) we discussed this problem in detail, and showed what happens, in large samples, to information estimators in the non-stationary case; we argued that such estimators may be useful even when mutual information is no longer well defined.

Multiple Neurons

Many laboratories are now recording groups of neurons simultaneously, across multiple electrodes, which raises the tantalizing possibility of understanding the coordinated activity of neural networks. One of the issues in multi-neuron analysis involves the extent to which correlated activity contributes stimulus-related information beyond that available by assuming the neurons act independently. This has generated considerable interest and debate. Correlations may occur at fine time scales of only a few milliseconds, or at much broader time scales of tens to hundreds of milliseconds. Fine time scale synchrony could produce in a downstream neuron a sharp increase in probability of spiking, which many have argued ought to play a fundamental role in perceptual information transfer. Statistically, assessing fine time scale synchrony is a delicate matter because synchronous events are relatively rare so that uncertainty may be substantial and small biases could have a dramatic effect. Broad time scale correlation, reflecting more erratic network bombardment of multiple neurons, would also be of interest, especially to the extent that it may contain stimulus-related information. The challenge then is to describe the stimulus-dependence of dynamic interactions among multiple non-stationary point processes.

A simple way to assess dependence between two neurons, at relatively coarse time scales, is to compute the correlation between their spike counts over some time window. Recent neurophysiological literature documented a tendency for this correlation to increase as the length of the time window increases. Kass and Ventura (2006) showed that this phenomenon is a necessary consequence of multiplicative trial-to-trial variability. Not only did this result provide a new interpretation, and highlight the importance of specifying the time window in any discussion of correlation, but, because multiplicative models fit an important feature of spike train data, it also provides support for the use of loglinear models of intensity (having effects that are additive in the log probability scale). In Behseta et al. (2009) we developed a new correction for attenuation of correlation in the presence of measurement error, using Bayesian estimation in a simple hierarchical (random-effects) model, and showed it improved dramatically on existing alternatives in the psychology literature (to which standard regression errors-in-variables methods reduce when applied to correlation). For the neural spike count data we analyzed, correction for attenuation changed the estimated correlation substantially, making it much more consistent with experimental prediction. Building on the ideas in Kass and Ventura (2006), and building on the hierarhical modeling approach of Behseta et al. (2009), Vinci et al. (2016) provided a thorough treatment of spike count correlation, separating correlation due to trial-to-trial variation from that due to within-trial variation. In Vinci et al. (2016), interest shifts from spike count correlation to correlation of the underlying firing rates (the normaized expected values of the spike counts). Vinci et al. (2018a) showed that when graphical LASSO is used to regularize the covariance matrix from multiple neuron spike counts the covariance matrix is not estimated well, and in particular, the zero partial correlations are poorly identified (on average, not much better than chance), but if physiological covariates are used to adjust the regularization performance improves dramatically. Vinci et al. (2018b) then combined the adjusted-regularization approach of Vinci et al. (2018a) with the hierarchical modeling approach of Vinci et al. (2016) to provide a latent-variable method that does a good job of estimating underlying firing rate correlations and the resulting graphical model.

Spike count correlation applies to large time windows (tens to hundreds of milliseconds). As mentioned above, there has also been intense interest in the physiological significance of near-synchronous firing within trials, which may be assessed using histogram methods and the cross-correlogram. These techniques are useful but do not allow for measured sources of variation (which would appear as covariates in the regression framework), including trial-to-trial variation. Ventura, Cai, and Kass (2005a) developed a trial-averaged point process regression method using BARS and bootstrap methods, showing that it is substantially more powerful than histogram methods, and Ventura, Cai, and Kass (2005b) adapted this approach to accommodate trial-to-trial variation.

An important source of trial-to-trial variation may be captured from the overall activity of the many neurons recorded across an electrode array. Using more than 100 simultaneously recorded spike trains from primary visual cortex (V1), Kelly, Smith, Kass, and Lee (2010a) showed how local field potentials (LFP), which are slowly-varying voltage responses thought to represent synaptic activity in the surrounding network, can be highly correlated with network activity. Accounting for such activity via LFP can improve estimation of stimulus-related neural response. Kelly, Smith, Kass, and Lee (2010b) extended these ideas using L1 regularized point process models to summarize the network effects arising from dozens of simultaneously recorded neurons.

The point process regression approach of Ventura, Cai, and Kass (2005a,b) was aimed at assessing synchrony (i.e., the extent to which synchronous spiking deviates from that produced by point process noise), and relating it to covariates. This idea was generalized and put on a more solid theoretical foundation by Kass, Kelly, and Loh (2011) and Kelly and Kass (2012). Just as individual spike trains form binary time series, a pair of simultaneously-recorded spike trains forms a time series of 2 by 2 tables (with four entries at each time point for the four combinations of spiking or not spiking across both neurons). In general, the spike combinations from n neurons will form a time series of 2^n tables. A statistically natural approach to analyzing these spike combinations, and to look for excess synchronous spiking, is to apply loglinear modeling technology, and many previous authors did so. The standard approach, however, has two shortcomings. First, it assumes stationarity of firing rates across suitable time intervals. Second, it does not incorporate spiking history, or other covariates, and therefore effectively assumes Poisson spiking. In addition, the standard approach ignores the inherent relative sparsity of two-way and multi-way synchronous spiking. Kelly and Kass (2012) provide a modification to the usual loglinear modeling methodology to accommodate time-varying firing rates and/or non-Poisson history effects and/or time-varying covariates (representing phenomena such as network activity). This results in a blend of loglinear modeling with point-process regression. Scott et al. (2015) showed how large numbers of pairs can be analyzed using Bayesian control of false discoveries (100 neurons gives over 8,000 pairs which would be subject to examination for excess synchrony). Zhou et al. (2016) used the framework of Kass, Kelly, and Loh (2011) and Kelly and Kass (2012) to give a rigorous statistical method for assessing the association between oscillations (in a local field potential) and neural synchrony.

The use of point processes to describe and analyze spike train data, together with the observation that point processes may be considered, approximately, to be binary time series, has been one of the major contributions of statistics to neuroscience. Neuroscience and statistical theory reside in continuous time, while measurements are made and data are analyzed in discrete time. The formal connection between continous time and discrete time is made by passage to the limit as the discrete bin size converges to zero. In trying to make a similar formal connection for multiple binary time series, however, a puzzle emerges: the standard regularity conditions in point processes forbid simultaneous events. How then can we construct point process approximations to multivariate binary time series where simultaneous events are not only allowed but, in fact, a main focus of interest? Kass, Kelly, and Loh (2011) provided a solution to this problem through the introduction of a sequence of point processes (marked processes) that satisfy hierarchical sparsity, according to which 2-way spiking is rare relative to 1-way spiking, 3-way spiking is rare relative to 2-way spiking, etc. This contributes a framework for thinking about synchrony, and it produces simple, intuitive estimators and significance tests for effects of excess multiway synchronous spiking. The problem of synchrony detection, and its statistical subtleties, was reviewed by Harrison, Amarasingham, and Kass (2013).

Decoding and Brain-Computer Interface

Multielectrode neuronal recording not only helps advance a variety of basic scientific efforts, it also has clinical applications of potentially great importance through neural prostheses using brain-computer interfaces (BCIs). These methods have advanced furthest in motor control. The idea here is that an array of electrodes implanted in a suitable brain region can record enough neurons that by simply thinking about an arm movement, a severely-disabled subject will produce neuronal activity sufficient to drive a robotic device in place of a non-functioning arm or hand. Beneficiaries of such devices could include people paralyzed by head or spinal cord trauma, and those with deficits caused by stroke, ALS (``Lou Gehrig's Disease''), cerebral palsy, or multiple sclerosis. In fact, a paper in Nature from the lab of our colleague Andrew Schwartz reported that monkeys can learn to use neural-prosthetic robotic devices to feed themselves, and a follow-up in Lancet reported that a tetraplegic human could manipulate objects with a BCI-driven robotic arm. For several years prior to the human studies, my statistical colleagues and I collaborated extensively with the Schwartz lab, partly to understand and optimize the neural prosthetic algorithms, and partly to use BCIs for scientific investigation.

Brain-computer interfaces for motor control use decoding algorithms to predict movements from patterns of neural activity. Neurons in primary motor cortex, for example, display directional tuning, meaning that their firing rate increases when arm or hand movement is in a particular direction; once such neural encoding is learned, statistically, it may be decoded to predict movement. We and others have developed and studied efficient decoding algorithms based on state-space models.

Brockwell, Rojas, and Kass (2004) showed how Bayesian sequential decoding, based on state-space models (dynamic models that generalize the Kalman filter) could be far more efficient than the usual method known as the population vector algorithm. However, in that work we used particle filtering, which can be extremely slow--potentially too slow for real-time prosthetic decoding. Koyama, Castellanos, Shalizi, and Kass (2009), developed and studied what we called the Laplace-Gauss filter, which is based on a normal approximation to the posterior together with an application of Laplace's method, to provide a fast computational method for non-Gaussian and/or non-linear state-space models. Emery Brown and co-workers had previously used a similar approach in related applications. We streamlined the implementation, proved that the method was asymptotically valid in not accumulating errors across time, and showed that it could be two orders of magnitude faster than particle filtering. We also investigated its use in prosthetics, and Koyama, Chase, Whitford, Velliste, Schwartz, and Kass (2009) showed that the subject can correct for the excess bias in the population vector algorithm when it becomes apparent visually, but not the excess variance. Chase, Schwartz, and Kass (2009) provided additional detail and interpretation of bias correction.

Part of the purpose of these efforts has been to better understand adaptation and learning within motor cortex. In BCI experiments the neurons that drive movement (of a cursor on a computer screen, or of a robotic hand) are under experimental control. Jarosciewicz, Chase, Fraser, Velliste, Kass, and Schwartz (2008) showed that rotational perturbations of the mapping between neurons and cursor movement created a small but statistically discernable change, preferentially, across the population of neurons whose mapping had been perturbed when compared with the remaining population of neurons where the mapping had been left intact. The change in motor cortical neural firing could have involved both changes in inputs, as the subject sought to counter the perturbation, and changes in individual neural tuning curves. Chase, Schwartz, and Kass (2010) introduced latent ``re-aiming targets'' to help separate these effects and showed this to improve estimation of neural tuning curves. Re-analysis of the Jarosciewicz et al. data supported the original findings.

Much modeling in the brain sciences pursues the idea that neural systems may behave optimally in the sense of using Bayes' Theorem for inference. An important theoretical contribution (by Ma and colleagues) was to show that neural systems could, in principle, combine information from two sources just as would be required according to Bayesian inference. In Orellana, Rodu, and Kass (2017) we noted that population vectors, which are based on linear models and are clearly computationally feasible by neural systems, could be used in much the same way. In limited circumstances these form a special case of that considered by Ma and colleagues, and they are actually optimal. Even though combining information with population vectors is, in general, sub-optimal, we raised the possibility that this simpler neural methodology might be more robust to errors in synaptic weights.